Your cart is currently empty!
Tag: Siglent Oscilloscopes
Generating an Activation Code (Option Code)
Introduction
Many SIGLENT products have options that can be activated by entering a special activation code into the front panel.
This note covers how to generate the activation code.
Setup
- Contact your Authorised SIGLENT sales office or distributor to obtain an Option Card. This is typically a document that is emailed as a PDF.
A typical Option Card will contain the following information:
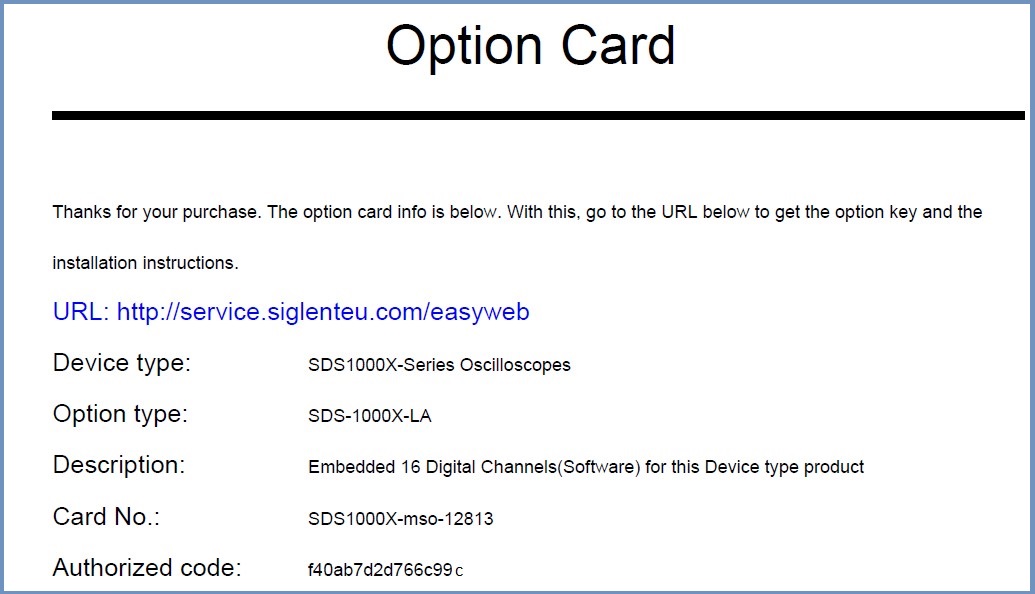
This is the official SIGLENT website for generating activation codes.
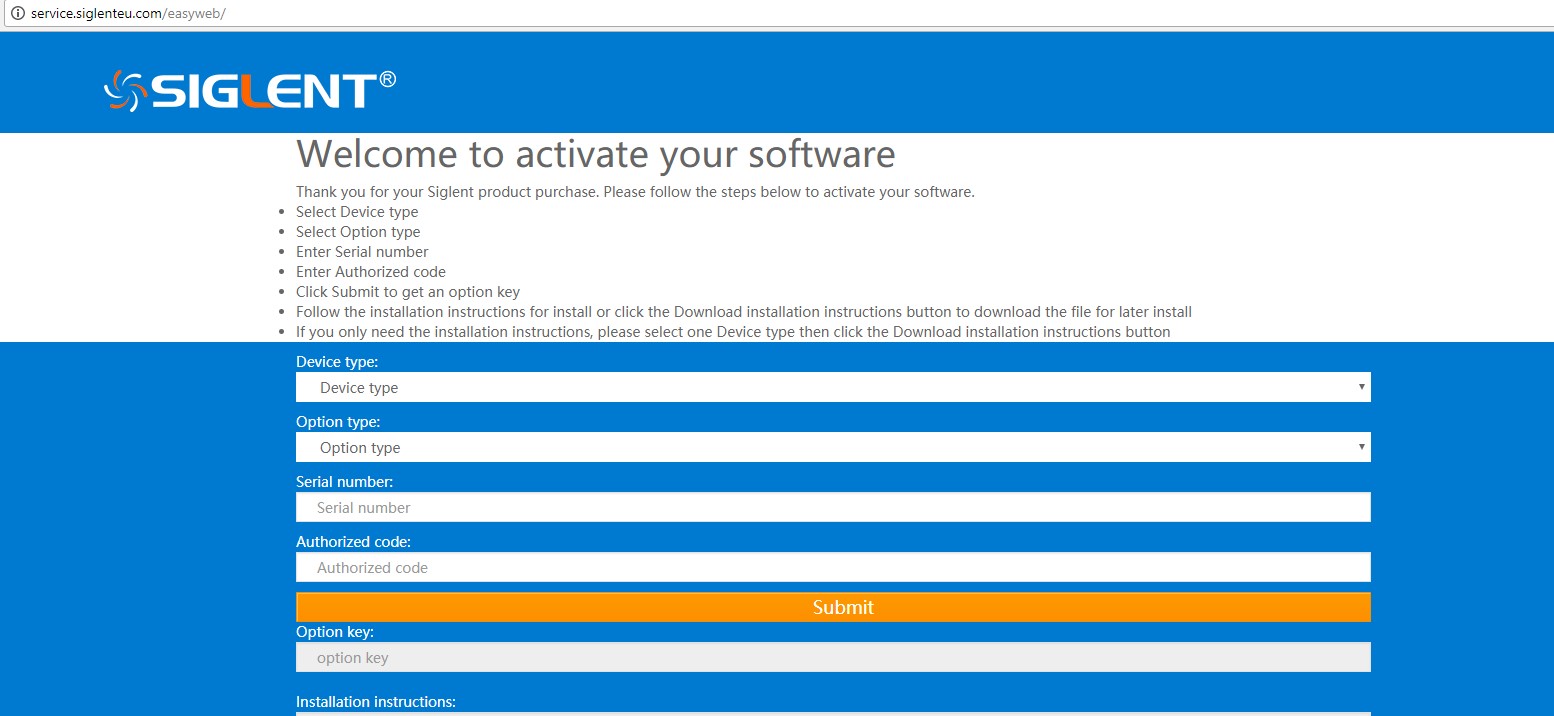
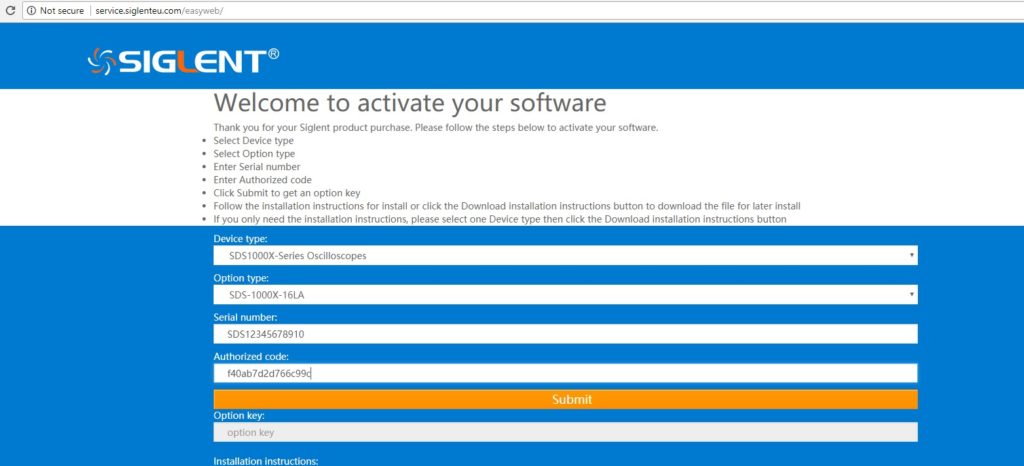
- Select the Device Type (Product Model Family)
- Select the Option Type (The option card you purchased)
- Enter the Serial Number of the instrument you wish to add the option to
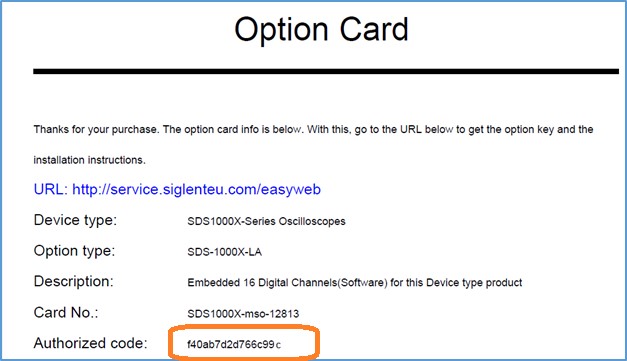
- Enter the Authorisation Code from the Option Card (example circled below).
- Press Submit. This will generate the Option Key which can be entered into the instrument and permanently activate the option.
NOTE: See the specific instrument user’s manual for instructions on entering option codes
EasyPulse Technology and Its Benefits
INTRODUCTION:
The majority of modern arbitrary/function waveform generators utilise DDS technology (Direct Digital Synthesis), but there are a few obvious defects using this technology directly. To solve these disadvantages, SIGLENT invented a pulse generating algorithm called EasyPulse technology. In this note, we will describe the basics of DDS and how EasyPulse can help get the best performance possible.
1.DDS technology and its disadvantages
Direct digital synthesis (DDS) is a technique to produce an analogue waveform (square, triangular, or sinusoidal) by generating a digital time-varying signal in digital form and then performing a digital-to-analogue conversion. A basic Direct Digital Synthesizer consists of a frequency reference (often a crystal or oscillator), a numerically controlled oscillator (NCO) and a digital-to-analogue converter (DAC), the block diagram is shown in Figure 1.
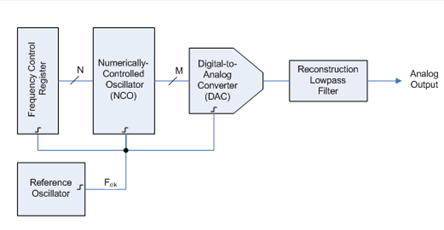
Figure 1: Block diagram of DDS circuit The reference clock is a fixed frequency (Fref). DDS generates the waveform by looking up the pre-loaded 2N data samples from memory.
The Tuning word (M) stored in the register determines the frequency of the output:
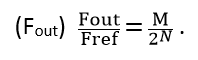
Since the edges of square/pulse signals output through the DDS technology are fixed, and the duty-cycle is limited by the data length, there will be poor duty-cycle setpoint resolution at higher output frequencies.
When generating a square/pulse, the reference frequency should be an exact integral multiple of the output frequency. If it is not an exact integral multiple, it will introduce a deterministic jitter equal to one reference clock period.
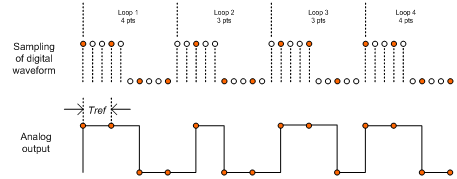
Figure 2 When the Tuning word >1 (i.e. Fout >Fref /2N ), some points in the sample lookup table are skipped. This is generally not a big problem for sinusoidal waveforms, but for arbitrary waveforms with some important details (e.g. spikes), it may mean the loss of information.
2.EasyPulse technology and its benefits
To solve these problems, Siglent invented a pulse generating algorithm called EasyPulse, which is applied to all of the SDG X series waveform generators.
Based on this new technology, the SDG series waveform generator is capable of generating a pulse signal with low jitter, rapid rising and falling edge (independent from frequency), small duty cycle( pulse width), edge and pulse width can be adjusted in a wide range. Figure 3 is the block diagram of EasyPulse:
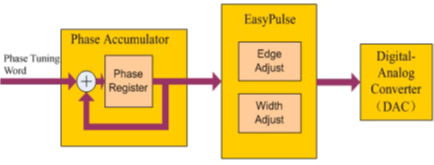
Figure 3: Block diagram of EasyPulse Take the SDG6052X series Pulse/Arbitrary Waveform Generator as an example, its specification for a pulse signal are as follows:
 3.Measurement examples
3.Measurement examplesEquipped with the EasyPulse technology, the SDS6052X series Pulse/Arbitrary Waveform Generator delivers great performance. Let’s take a look at some real-world examples:
First and foremost, the EasyPulse technology could overcomes the additional jitter in Square/Pulse waveform generated by traditional DDS. To evaluate this excellent feature, we compared a DDS waveform generator with the SDG6052X with EasyPulse. In figure 4, we used a 12-bit scope to observe the differences. When the Pulse is trigged, measuring the next rise edge, we observe a 0.84 ns (which is equal to the period of the DDS clock, 1.2 GHz) peak-peak jitter if the pulse is generated by traditional DDS, while the jitter downs to 11.2 ps rms when we choose EasyPulse technology to generate the pulse with same configuration.
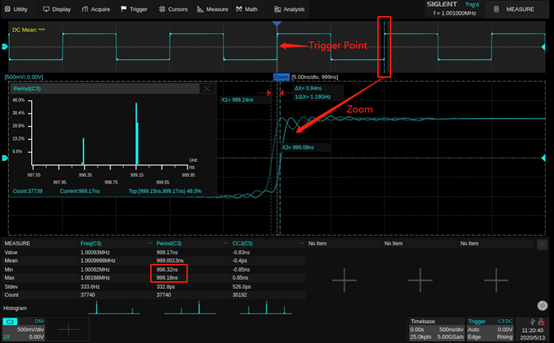
Figure 4: Jitter from a traditional DDS waveform 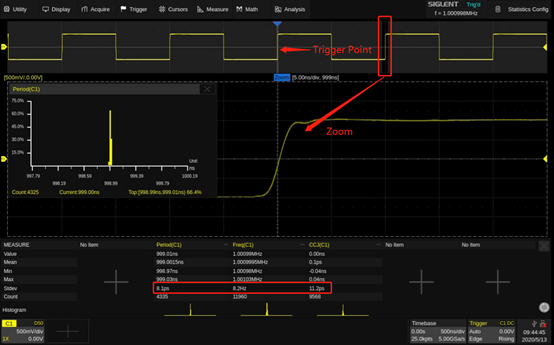
Figure 5: EasyPulse waveform with low jitter Another advantage of the EasyPulse technology is its ability to output the pulse with a small pulse width around 3.3 ns, even at very low frequency. For a 1 Hz pulse generated by DDS technology, there are 32768 points in one waveform length. If we built the pulse with only one sample point at the high level, we could get a pulse with the minimum pulse width (minimum duty ratio as well), which is about 30 ms (1 s/32768 ≈ 30.5 ms), as shown in figure 6. With EasyPulse, the width can be adjusted down to 3.3 ns as shown in figure 7.
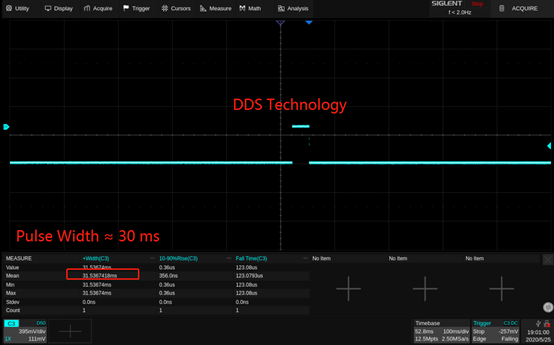
Figure 6: 1 Hz pulse signal generated by DDS 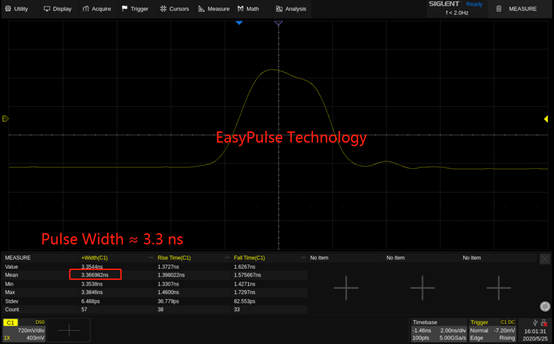
Figure 7: 1 Hz pulse signal generated by EasyPulse In addition, with the EasyPulse technology, both the edge and pulse width can be adjusted over a wide range. The pulse width can be fine-tuned to the minimum of 3.3 ns with an adjustment step as small as 100 ps, at any frequency. In figures 8 and 9, we used a 12-bit scope with infinite persistence to show the rising edge changes with pulse width settings from 3.4 ns to 200 ns with 100 ps each step.
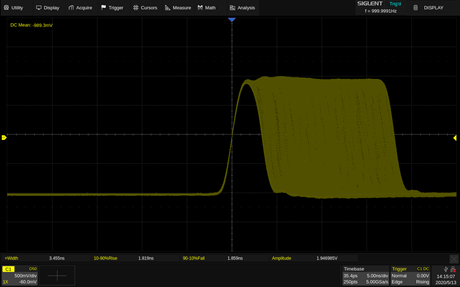
Figure 8: Adjusting the pulse width with 100 ps each step The rise/fall times can also be set independently to the minimum of 1 ns at any frequency with a minimum adjustment step as small as 100 ps. Output an initial pulse by the SDG6052X as the following parameters:
Figure 9 shows the rising edges of the SDG6052X Pulse/Arbitrary Waveform Generators from 1.0 ns to 100.0 ns step by step with 100 ps.
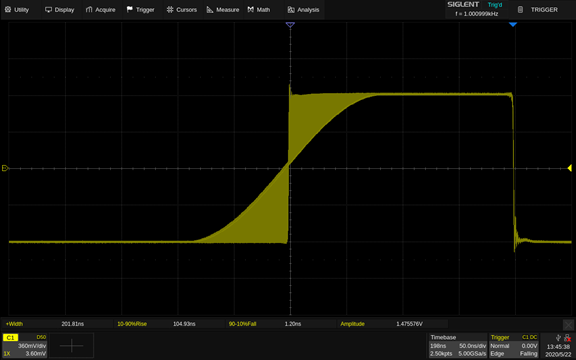
Figure 9: adjusting the rise time with 100 ps each step In conclusion, EasyPulse technology enables SIGLENT Pulse/Arbitrary Waveform Generators to perform excellently when generating a pulse signal with low jitter, small duty cycle, precise and adjustable pulse width.
Products Mentioned In This Article:
Analysing GSM Radio Protocol with a Siglent SDS2000X Plus Oscilloscope
We took a retired Siemens A36 cellphone to learn the capabilities of this new Siglent scope. Available documentation and medium-density PCB of the selected A36 made the signal probing easy to implement. We used TEK P6243 active probes initially for their low capacity loading but changed to passive probes later as monitored signals proved to be quite robust.
 Figure 1: probing IQ signals in Tx and Rx path of the Siemens A36
Figure 1: probing IQ signals in Tx and Rx path of the Siemens A36Three signals were selected to monitor the cellphone operation:
- Transmit IQ baseband modulation signal, Q component, on Pin 48 on scope Channel 1
- Receive IQ baseband modulation signal, I component, on Pin 12 on scope Channel 2
- Battery current consumption from 0.1 Ohm resistor, between (-) power supply and phone ground on scope Channel 4 (resulting in negative signal polarity)
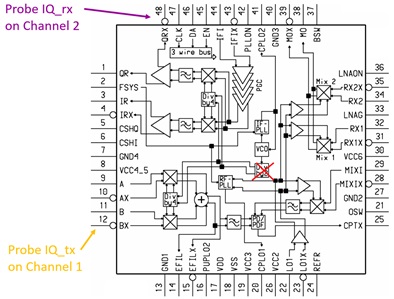
Figure 2: block diagram of PMB6250 Smarti IC with probe inputs
At first we observed the phone attached to the GSM network, periodically listening for an eventual incoming call on paging channel once per second. Once every 33 seconds, the phone is additionally checking the signal level of other base stations to request the network to camp on the stronger base station in the case when the phone is moving.
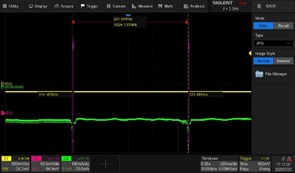
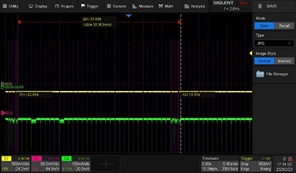
Figure 3: Rx signals for paging (left) and neighbour cell measurements (right)
Current peaks of 30 mA at the end of Rx signal burst indicate the processing power needed for decoding of the received signal. Neighbour channel measurement need only a part of the burst, allowing for frequency switching (PLL re-tuning) between the 3 bursts. We can see how noisy the other base stations are, and that the first burst of the serving base station has the least noise of all.
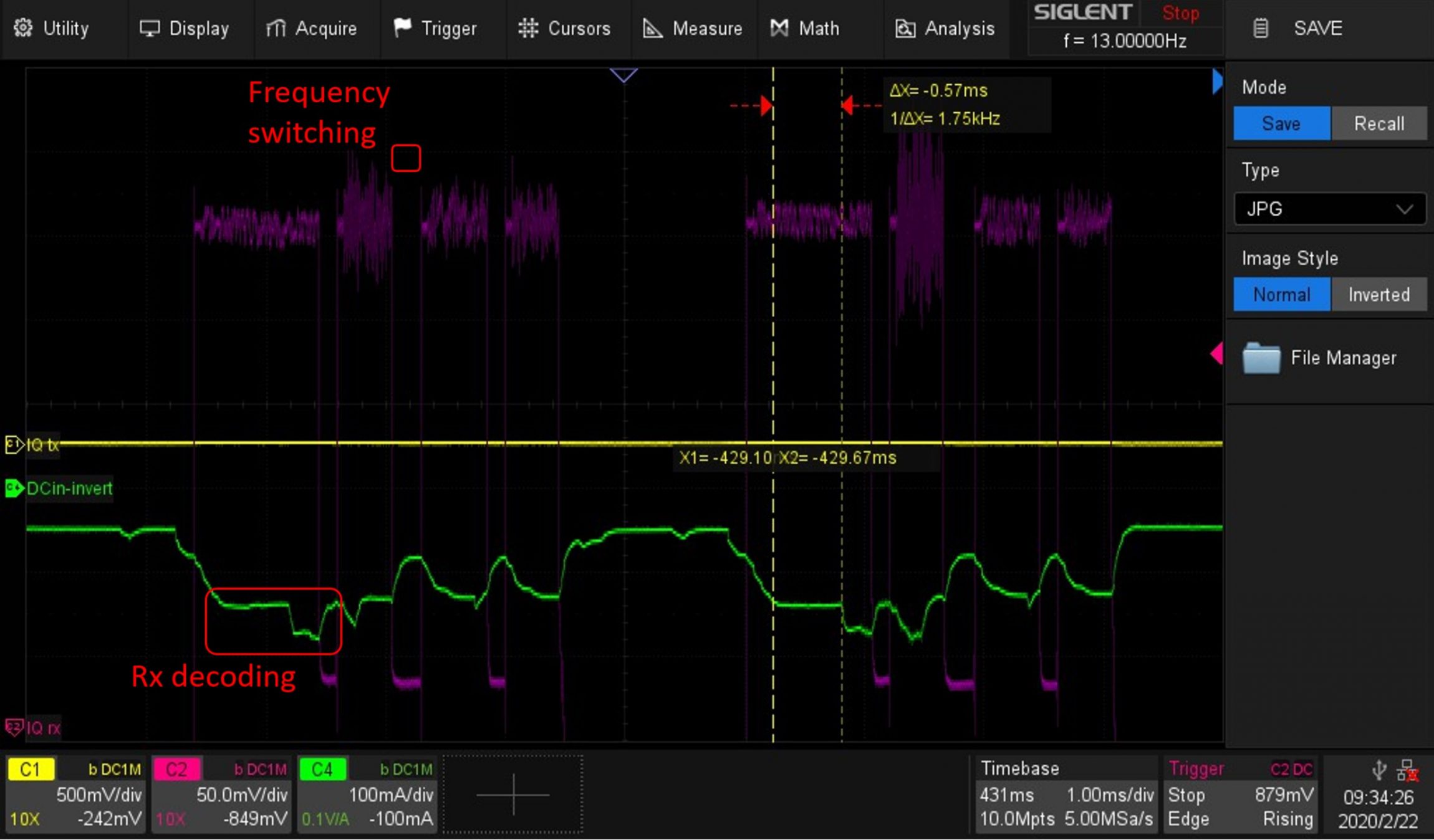
Figure 4: Rx signal detail and processing power (power consumption)
Using the scope persistence and colour histogram, we can visualise the received signal. We also used the scope Zone Trigger function (area 1) to distinguish between the longer data and shorter paging channels. We see the signal reception is longer than the data burst length of 570 µs. This allows for the demodulation of signals that may be dealing with multipath propagation. In a mountainous region, for example, base station signals can reach the phone on the direct fast track but may also propagate along a path with multiple reflections. Up to +-3 symbols delay can be processed by the A36 channel equaliser.
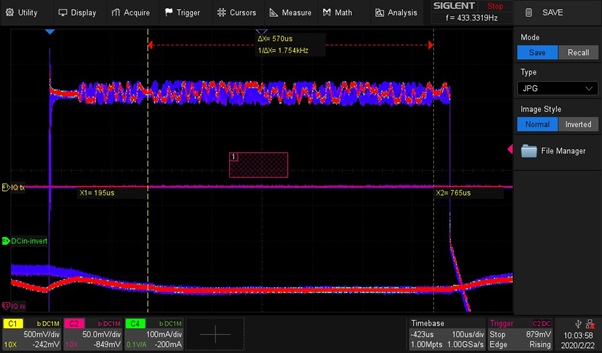
Figure 5: Histogram of Rx signal with 1 sec persistence
Then we set up a call between the phone and the network. For the first time, we can see the phone transmitter operation (yellow Channel 1). As the phone receives an incoming call from the paging channel it changes from idle to the call state after the user picks up the call of the ringing phone.
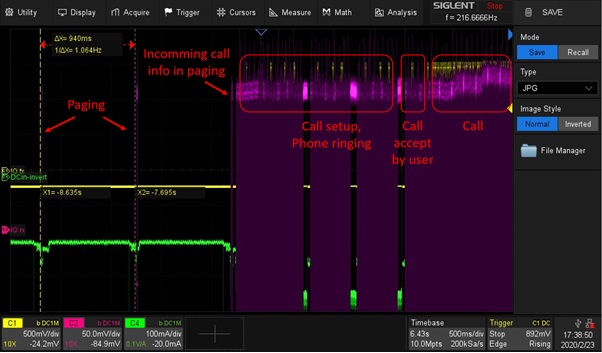
Figure 6: Incoming call setup flow
Parallel to the call, the phone still performs neighbour cell measurements for the case it finds a stronger base station that can handover the call.
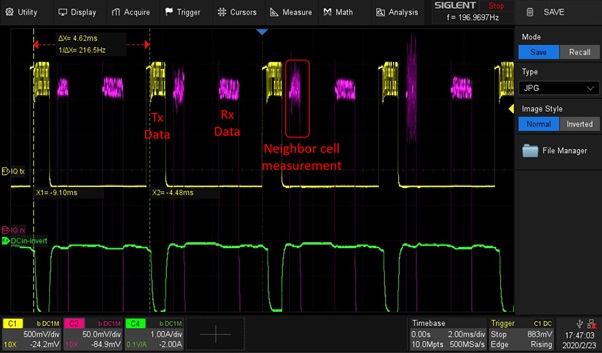
Figure 7: Call Tx and Rx bursts
On the transmit burst we can observe the permanently changing data bits carrying the speech signal. The static non-changing bits are the Tail Bits at the beginning and the end of the burst. Most important is the Training Sequence in the middle of the burst. The channel equaliser of the receiver is training its best adjustments on this training sequence and use this adjustment for the whole burst. The training sequence is in the middle of the burst, while the propagation conditions are changing as the phone is moving and the position in the middle of the burst is best for the whole burst. 1-second persistence, colour histogram and zone trigger features of the scope are used to visualise this dynamic situation.
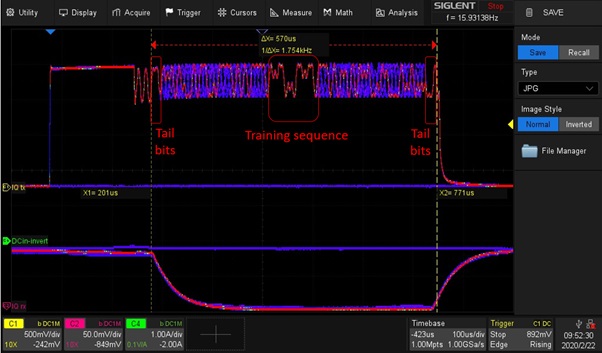
Figure 8: Histogram of Tx signal with 1-sec persistence
Peak current of almost 2 A at 4 V DCin covers the demand of the Tx power amplifier. During the reception of a call, the peak current is 100 mA. There is no measurable power consumption between the Rx paging reception, the implemented Eco-Mode only powers the 32 kHz clock inside the phone to wake-up the phone for the next paging. That’s why the battery charge can last for many days if no calls performed.
Large memory depth of the scope was very helpful to zoom-in into the captured data. Various trigger options helped to get a stable trigger for fast-changing signals.
We were extremely surprised by the good performance and rich features of the new Siglent SDS2000x Plus oscilloscope. The performance of this mid-class entry model is on the level of high-end units back in the time when one of the authors designed the A36 phone. We recommend this scope to all interested readers and look forward to checking LTE and 5G phones with this scope in our next projects.
Products Mentioned In This Article:
- SDS2000X Plus series please see HERE
Programming Example: Retrieve data from an XE series Oscilloscope using Kotlin
The SDS series of oscilloscopes all feature remote programming and data collection capabilities. They can be integrated easily into many automated test environments to ease the setup and data acquisition during testing.
One of our helpful customers developed a nice programming example designed to set up and retrieve data from a SIGLENT SDS1202X-E Oscilloscope using Kotlin, a free open source coding environment (more on Kotlin here).
The code utilizes a LAN connection and open sockets.
Thanks to Chris Welty for the code!
Here is a text file of the example:
/**
* License: 3-Clause BSD
*
* Copyright 2018 Chris Welty
*
* Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
*
* 1. Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer.
*
* 2. Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.
*
* 3. Neither the name of the copyright holder nor the names of its contributors may be used to endorse or promote products derived from this software without specific prior written permission.
*
* THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS “AS IS” AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING,
* BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO
* EVENT SHALL THE COPYRIGHT HOLDER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR
* CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR
* PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY,
* OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE
* POSSIBILITY OF SUCH DAMAGE.
*/package scope
import java.io.BufferedWriter
import java.io.OutputStreamWriter
import java.io.Serializable
import java.net.Socket/**
* Contains a single waveform downloaded from a Siglent 1202X-E
*/
class Waveform(val vDiv: Double, val vOffset: Double, val tDiv: Double, val tOffset: Double, val data: ByteArray) : Serializable {val xs: DoubleArray
get() = DoubleArray(data.size, { i -> i * tDiv * 14 / data.size + tOffset – tDiv * 7 })val ys: DoubleArray
get() = DoubleArray(data.size, { i -> data[i] * vDiv / 25 – vOffset })companion object {
/**
* Download the waveform displayed on the scope’s screen
*/
fun download(): Waveform {
Socket(“192.168.1.222”, 5025).use { socket ->println(“connected to ” + socket.inetAddress)
val output = BufferedWriter(OutputStreamWriter(socket.getOutputStream(), Charsets.US_ASCII))// since the socket can return binary data, we can’t use an InputStreamReader to
// translate the bytes to characters. We’ll have to do it ourselves.
// SCPI generally uses US ASCII, shouldn’t be too hard.
val input = socket.getInputStream()/**
* Read from the scope until \n is encountered.
* The bytes are translated to characters numerically (so US_ASCII).
*/
fun readLine(): String {
val sb = StringBuilder()
while (true) {
val c = input.read()
when (c) {
-1, ‘\n’.toInt() -> return sb.toString()
else -> sb.append(c.toChar())
}
}
}/**
* Read a number of bytes from the scope.
*
* The bytes are not translated into characters.
*/
fun readBytes(n: Int): ByteArray {
val result = ByteArray(n)
var i = 0
while (i < n) {
i += input.read(result, i, n – i)
}
return result
}fun writeLine(string: String) {
output.write(string)
output.write(“\n”)
output.flush()
}/**
* Read a numerical response from the scope.
*
* The scope returns responses like “C1:VDIV 1.00E+00V”.
* This function extracts the “1.00E+00″, converts it to a double, and returns it.
*/
fun readNumber() = readLine().split(” “)[1].dropLast(1).toDouble()writeLine(“*IDN?”)
println(readLine())// reset the scope response format to its default so readNumber() works
writeLine(“CHDR SHORT”)writeLine(“C1:VDIV?”)
val vDiv = readNumber()writeLine(“C1:OFST?”)
val vOffset = readNumber()writeLine(“TDIV?”)
val tDiv = readNumber()writeLine(“TRDL?”)
val tOffset = readNumber()// request all points for the waveform
writeLine(“WFSU SP,0,NP,0,F,0”)
writeLine(“C1:WF? DAT2”)// parse waveform response
val header = String(readBytes(21))
println(“header is $header”)
val length = header.substring(13, 21).toInt()
println(“length is $length”)
val data = readBytes(length)
readBytes(2) // 2 garbage bytes at endprintln(“V/div = $vDiv; offset = $vOffset; t/div = $tDiv; tOffset = $tOffset”)
return Waveform(vDiv, vOffset, tDiv, tOffset, data)
}
}
}
}Products Mentioned In This Article:
Siglent Oscilloscopes please see HERE
Comparison / Differences between the SDS1000X and SDS1000X-E oscilloscope families
The short list of differences between the X and the 2 channel XE (SDSs1202XE) is as follows:– X has 50 ohm/ 1 MOhm selectable input impedance. XE only has 1 MOhm fixed. You will need a 50 ohm matching through adapter if you wish to connect to 50 Ohm circuits/minimize reflections.– The X has a slightly larger display (8″) vs. the XE (7″)– The XE has a faster digital platform with 1 Mpt FFT capability. The X has 16,384 pt depth for the FFT.In addition, the SDS1xx4X-E scopes have additional differences:– Onboard webpage control (standard)– Bode Plot (standard.. requires SIGLENT SDG or SAG1021)– External waveform/function generator (SAG1021 and SDS1000X-E-FG license Optional)– WiFi control (TL-WN725N and SDS1000X-E-WiFi license Optional)Products Mentioned In This Article:Programming Example: List connected VISA compatible resources using PyVISA
PyVISA is a software library that enables Python applications to communicate with resources (typically instruments) connected to a controlling computer using different buses, including: GPIB, RS-232, LAN, and USB.
This example scans and lists the available resources.
It requires PyVISA to be installed (see the PyVISA documentation for more information)
***
#Example that scans a computer for connected instruments that
#are compatible with the VISA communication protocol.
#
#The instrument VISA resource ID for each compatible instrument
#is then listed.
#
#
#Dependencies:
#Python 3.4 32 bit
#PyVisa 1.7
#
#Rev 1: 08302018 JCimport visa
def main():
rm = visa.ResourceManager()
print (rm.list_resources())if __name__==’__main__’:
main()
*****
Here is the code:
And here is the result of a scan:
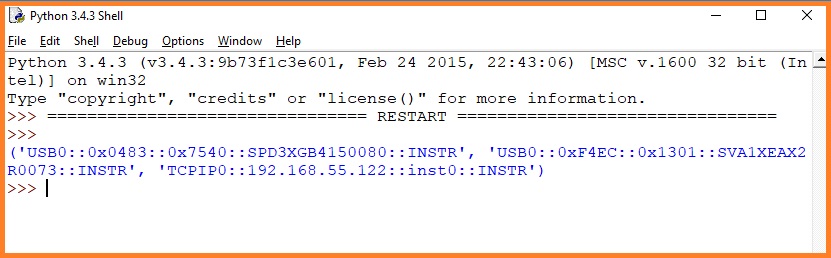
Each connected instrument returns a specific formatted string of characters called the VISA Resource ID.
The resource ID format is as follows:
‘Communication/Board Type (USB, GPIB, etc.)::Resource Information (Vendor ID, Product ID, Serial Number, IP address, etc..)::Resource Type’
In the response, each resource is separated by a comma. So, we have three resources listed in this example:
‘USB0::0x0483::0x7540::SPD3XGB4150080::INSTR’ – This is a power supply (SPD3X) connected via USB (USB0)
‘USB0::0xF4EC::0x1301::SVA1XEAX2R0073::INSTR’ – This is a vector network analyser (SVA1X) connected via USB (USB0)
‘TCPIP0::192.168.55.122::inst0::INSTR’ – This is an instrument connected via LAN using a TCPIP connection at IP address 192.168.55.122
Products Mentioned In This Article:
SDS FFT performance on low frequency signals
Like many modern oscilloscopes, the SIGLENT SDS series feature FFT math functions that calculate frequency information from the acquired voltage vs. time data. FFT stands for Fast Fourier Transform, and is a common method for determining the frequency content of a time-varying signal. Converting time domain data to the frequency domain makes measuring characteristics like phase noise and harmonics much easier. Oscilloscopes don’t have the dynamic range or sensitivity of a true spectrum analyser, but these new designs can provide a fine level of detail that may be just enough for your application.
FFTs are commonly used on high frequencies, but they can also be used on signals with fairly low frequencies.
In this note, I am going to show the FFT performance of two series of our scopes by sourcing a 10 MHz (100 s period), 10 Vpp sine wave using a SIGLENT SDG805 Function Generator into Channel 1.
SDG805 has been discontinued, to see other models in the SDG800 series please click HERE
SDS1000X/SDS2000X Series:
The SDS1000X and 2000X series feature an FFT function that uses up to 16 kpts of timebase data to calculate the frequency data and a timebase maximum of 50 s/div.
Here are the FFT results with the available window settings for a 10 MHz sinewave –
The scope can show a split timebase and FFT view:
For the rest, I will use the exclusive FFT view.
Rectangle
Blackman
Hanning
Hamming
Flat Top
SDS1000X-E Series:
The SDS1000X-E series feature a new math co-processor that increases the maximum data depth of the FFT function to 1 Mpts. They also feature a timebase maximum of 100 s/div. These increases allow the X-E to have much finer timebase detail and to acquire useful data for even lower frequencies than many scopes on the market.
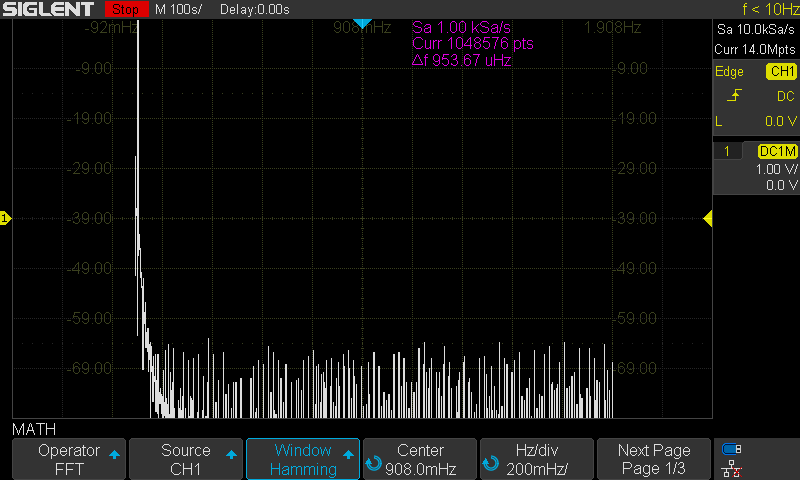
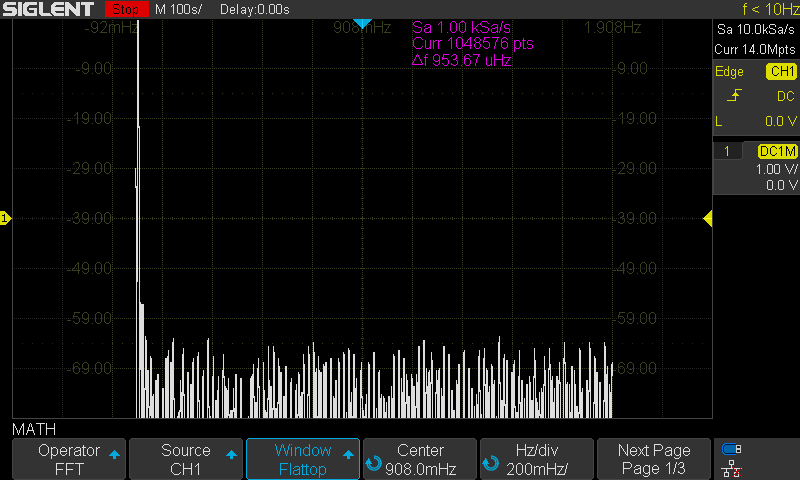
Here are the FFT results with the available window settings for a 10 MHz sinewave –
The scope can show a split timebase and FFT view:
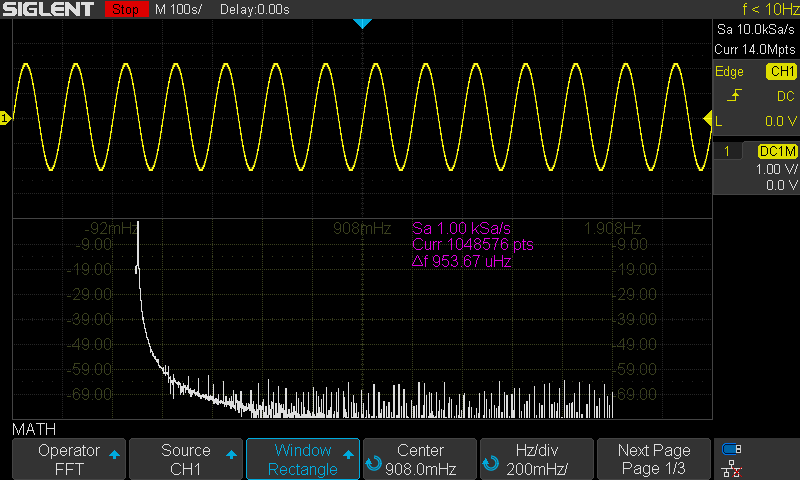
For the rest, I will use the exclusive FFT view.
Rectangle
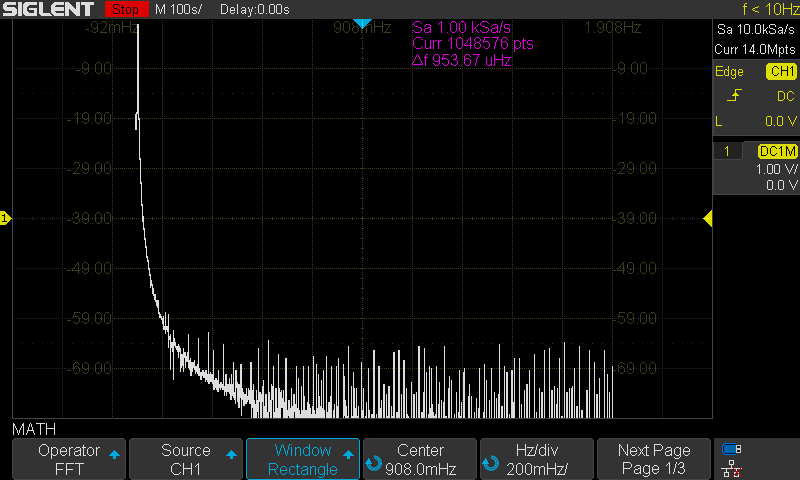
Blackman
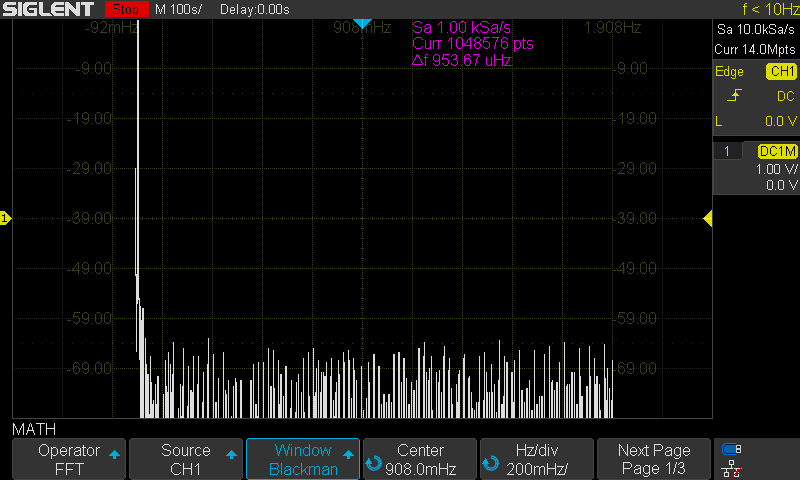
Hanning
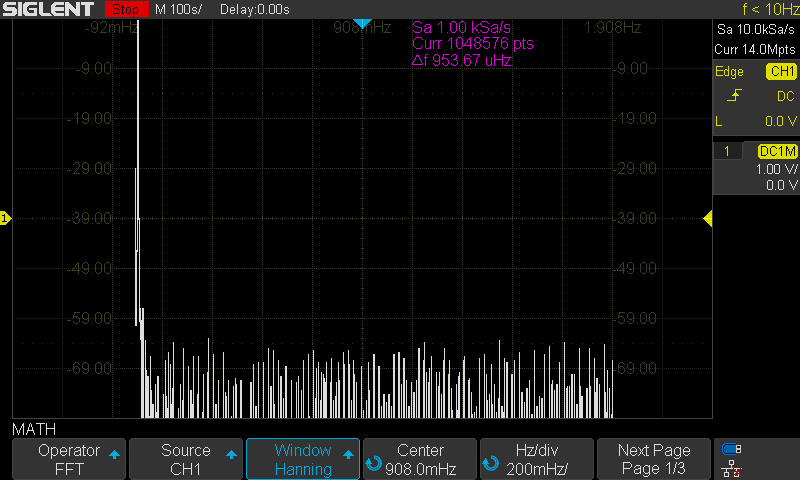
Hamming
Flat Top
Products Mentioned In This Article:
Programming Example: SDS Oscilloscope screen image capture using Python over LAN
Here is a brief code example written in Python 3.4 that uses a socket to pull a display image (screenshot) from a SIGLENT SDS1000X-E scope via LAN
and save it to the local drive of the controlling computer.NOTE: This program saves the picture/display image file in the same directory that the .py file is being run from. It will overwrite any existing file that has the same name.
Download Python 3.4, connect a scope to the LAN using an Ethernet cable, get the scope IP address, and run the attached .PY program to save a bitmap (BMP) image of the oscilloscope display.
Tested with:
Python 3.4
SDS1202X-E
SDS1104/1204X-E
SDS2000X-E Models
SDS5000X Models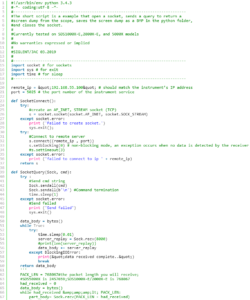

Measuring Power Supply Control Loop Response with Bode Plot II
Introduction
Stability is one of the most important characteristics in power supply design. Traditionally, stability measurements require expensive frequency response analysers (FRA) which are not always available in a laboratory. SIGLENT has released Bode Plot Ⅱ features to the SIGLENT SDS1104X-E, SDS1204X-E, SDS2000X-E, SDS2000X Plus, and SDS5000X series of oscilloscopes. When combined with a Siglent arbitrary waveform generator (SDG or SAG) and an injection transformer, quick frequency response curves can be created.
In this application note, we will show you the basic principles for making this stability measurement and how to use these instruments to make the measurement.
 Figure 1: Bode II setup
Figure 1: Bode II setup1. Basic Principle of Stability Measurement
1.1 Stability of The Feedback System
A regulated power supply is actually a feedback amplifier with a large amount of current sourcing capability. Any theory that applies to a basic feedback amplifier also applies to a regulated power supply.
In feedback theory, the stability of a feedback system can be determined by evaluating the loop transfer function. A more practical way is to measure the bode plot of the loop gain. Figure 2 shows a typical feedback system.
The closed-loop transfer A is the mathematical relationship between input x and output y. The loop gain T, by its name, is defined as the gain of a signal traveling around the loop.
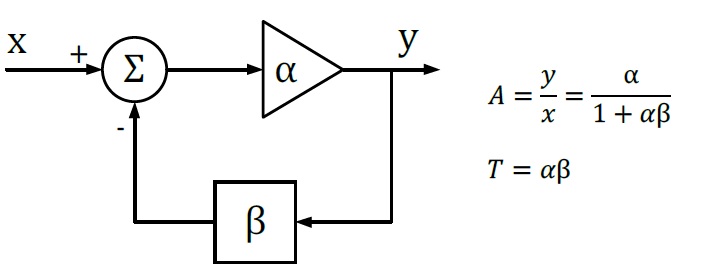 Figure 2: Typical Feedback Loop
Figure 2: Typical Feedback LoopSince α and β are complex variables, they have not only magnitude but also phase angle, as also does the loop gain T. If the phase angle of T reaches -180° while the magnitude is 1, the closed-loop transfer function A becomes infinity. In this situation, the system will maintain an output signal while there is no input. Thus, the system acts as an oscillator rather than as an amplifier, which means that the system is not stable.
If we plot the loop gain in a bode plot, we can evaluate the stability by finding the phase margin and gain margin. A phase margin is defined as how many degrees the phase can be decreased before reaching -180°while the magnitude is 1 (or 0 dB). The gain margin is defined as how many dB in magnitude can be added before reaching 1 (or 0 dB) while the phase is -180°.
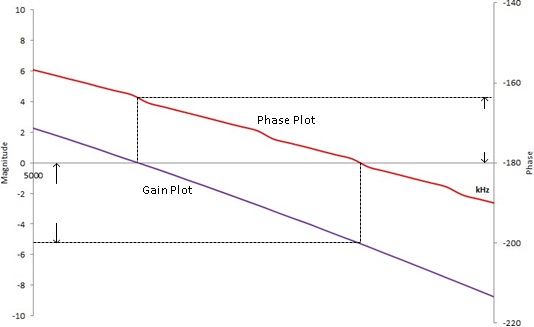 Figure 3: Bode Plot, phase, and gain margin
Figure 3: Bode Plot, phase, and gain margin1.2 Break the Loop
To get the desired loop gain, we simply break the loop. Figure 4 shows how to break the loop in a typical feedback system. Technically you can break the loop any place you like. We commonly choose to break the loop at the point between the amplifier output and the feedback network. Then we insert a test signal i to travel around the loop. The loop gain is the mathematical relationship between the output y and the test signal i.
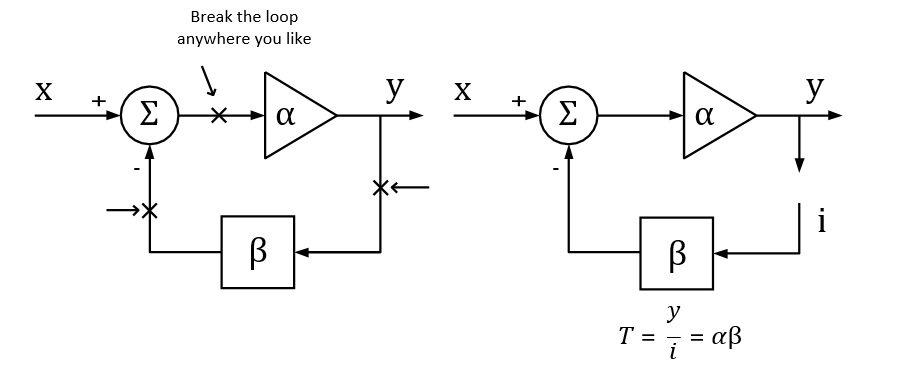 Figure 4: Breaking the loop in a typical feedback system
Figure 4: Breaking the loop in a typical feedback system1.3 Loop Injection
In reality, we can never really break the loop because the feedback loop serves to maintain the DC quiescent operation point of the circuits. Without the feedback loop, the device under test will become saturated because of the small input offset voltage, and then no useful result can be measured.
To overcome this, we should measure the open-loop response inside a closed loop. Therefore, we just inject a signal into the loop rather than breaking the loop. Figure 5 shows a typical method of loop injection. The injection point is chosen so that the impedance looking in the direction of the loop is much higher than that looking backward. One possible point is between the output and the resistor divider feedback network. Other points that meet this requirement may be chosen.
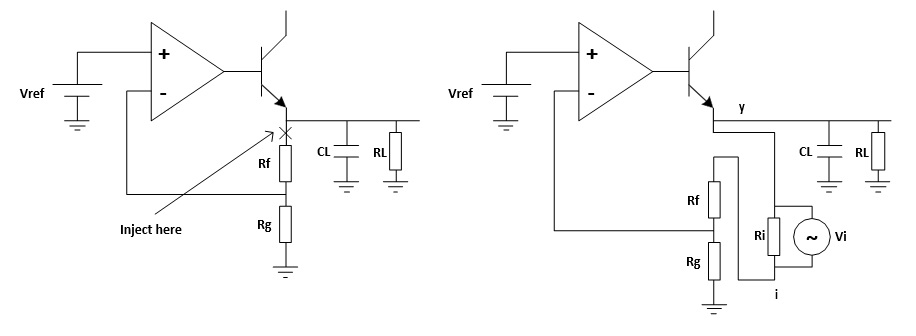 Figure 5: Loop injection
Figure 5: Loop injectionTo maintain the closed loop, a small injection resistor Ri is inserted at the injection point. The resistor should be small enough so that it will have little effect on the circuit and also the lower the resistor value the lower the frequency the transformer will operate. Picotest recommends a resistor value of 4.99 Ω for the J2100A, and a larger value may be chosen depending on the circuits. The injection signal is then applied across the injection resistor.
The signal injected should have no effect on the DC operating point of the circuit. A method to solve the common ground connection problem is to use an injection transformer as shown in Figure 6.
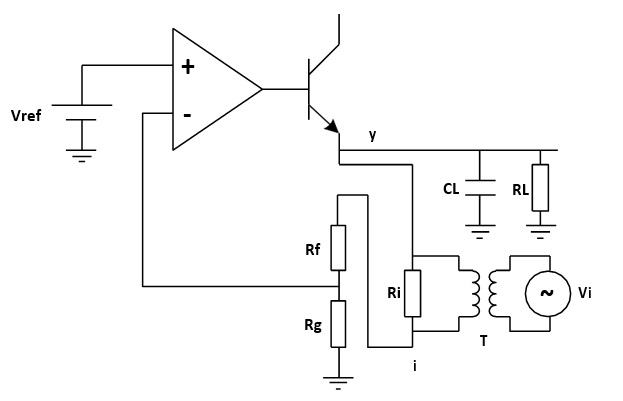 Figure 6: Injection Transformer
Figure 6: Injection TransformerThe injection signal starts at one end of the injection resistor, travels through the resistor divider feedback network, the error amplifier and the pass element transistor, and finally to the output, which is the other end of the injection resistor. The relationship between the injection signal i and the output signal y is the loop gain that we wish to measure.
Be aware that we are measuring an open-loop parameter inside a closed loop, the phase starts at 180°and decreases to 0°, rather than starting at 0°and decreasing to -180°. So the phase margin should be measured relative to 0°.
2. Measurement Setup and Result
2.1 Equipment
Oscilloscope: Siglent SDS1204X-E with firmware version higher than 6.1.27R1 (Bode Plot Ⅱ release)
Signal Source: Siglent SDG2042X
Power Supply: Siglent SPD3303X
Probe: Siglent PP215 passive probe switched to 1X
Injection Transformer: Picotest J2100A
Device-Under-Test: Picotest VRTS v1.51
2.2 Circuit Connection
The Picotest VRTS v1.51 is a demonstration board for voltage regulator testing. Technically it is a linear regulator built from the famous TL431 and a discrete transistor. The schematic is shown in Figure 7. Different output capacitors can be selected to see the impact on the control loop stability.
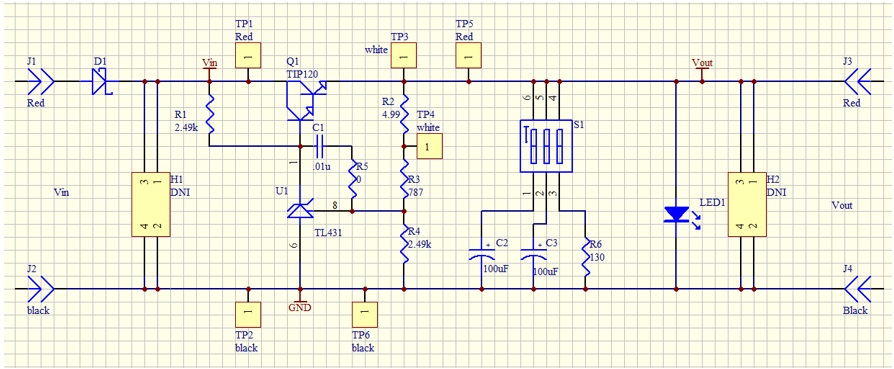 Figure 7: VRTS v1.51 schematic
Figure 7: VRTS v1.51 schematicFor the propose of our power supply control loop response measurement, the injection point is TP3 and TP4. The circuit connection is shown in Figure 8.
The generator is connected to the oscilloscope through USB (connection through Ethernet is also supported).
The injection transformer is connected in parallel with the injection resistor so that the signal is injected into the loop while preventing the circuit DC operation point from being affected by the generator.
The TP3 and TP4 points are also connected to the oscilloscope, and the TP4 is defined as the DUT Input while the TP3 is the DUT Output in the Bode Plot Ⅱ.
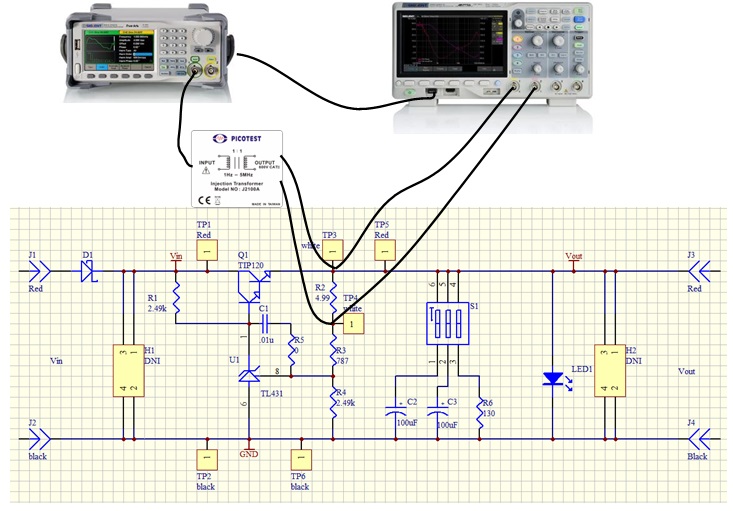 Figure 8: Circuit connection
Figure 8: Circuit connection Figure 9: Probe and Transformer connections to the DUT
Figure 9: Probe and Transformer connections to the DUT2.3 Instrument Configuration
In this section, we will show how the key configuration should be made in order to make the measurement correctly. For complete instructions to the Bode Plot Ⅱ, please refer to the user manual and the quick start guide.
Before entering the Bode Plot Ⅱ, it is recommended that you enable the oscilloscope’s 20 MHz bandwidth limit setting.
At this time, we want to measure the bode plot from 10 Hz all the way to 100 kHz. This frequency range should be enough for a circuit with an expected crossover frequency at about 10 kHz.
Enter the Config menu and set the Sweep Type to Simple, then enter Set Sweep to set the sweeping frequency. Set the Mode to Decade and Start to 10 Hz, Stop to 100 kHz. Set Points/dec to 20, enough for a typical sweep. Enter the Set Stimulus menu to set Amplitude to 50 mV. Enter the Set Channel menu to set DUT Input to CH1 and DUT Output to CH2.
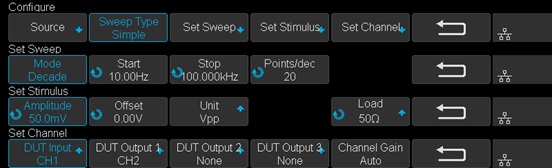 Figure 10: Bode II scope configuration
Figure 10: Bode II scope configuration2.4 Results and Data analysis
After the configuration is done, return to the main menu and press Run to start the sweep.
Wait to see the results as shown in Figure 11.
The result is somewhat confusing and suspect because of the trace at low frequency, especially the phase trace, alternating up and down. We will introduce a method called Vari-level to resolve this problem in the next section.
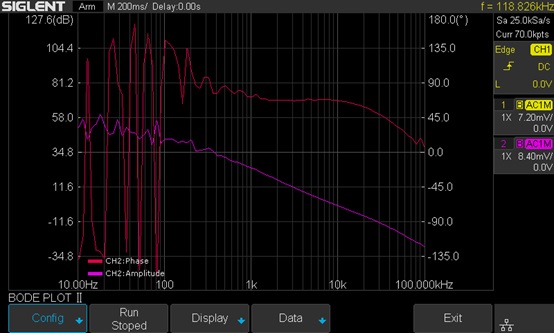 Figure 11: Measurement results
Figure 11: Measurement resultsAfter the sweep has completed, press Run again to stop the sweep. Enter the Display menu and then enter the Cursors menu to turn on the cursors. Use the Adjust knob to move the cursors and set the phase margin as shown in Figure 12.
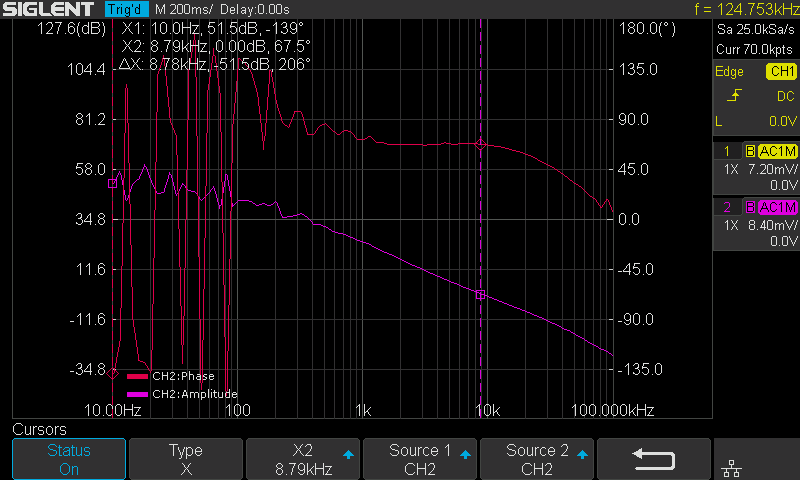 Figure 12: Cursor measurement on the Bode plot
Figure 12: Cursor measurement on the Bode plotYou can also turn on the List feature in the Data menu to examine the measured data, or you can export the data to an external USB FLASH driver for further analysis on a computer.
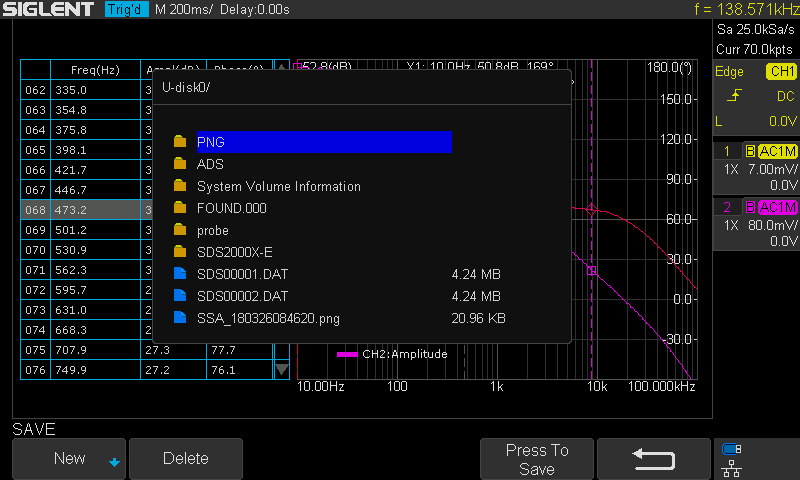 Figure 13: Exporting data
Figure 13: Exporting data2.5 Vari-level
In the previous section, we can see that the results are not ideal, for the bouncing trace at low frequency. This is because at low frequency the amplitude difference between the input and output channel is relatively large, and since we are using a relatively small stimulus signal (this time 50 mVpp), the signal presented at the DUT Input channel is extremely small so that a commercial general propose oscilloscope cannot measure it accurately.
But we cannot simply increase the stimulus’s signal amplitude. The result will be similar to what is shown in Figure 14. The large signal near the crossover frequency region causes serious distortion to the loop. The distorted signal in the time domain is shown in Figure 15.
Remember that a bode plot only makes sense in a linear system, and has no meaning in a heavily non-linear system. The result is useless.
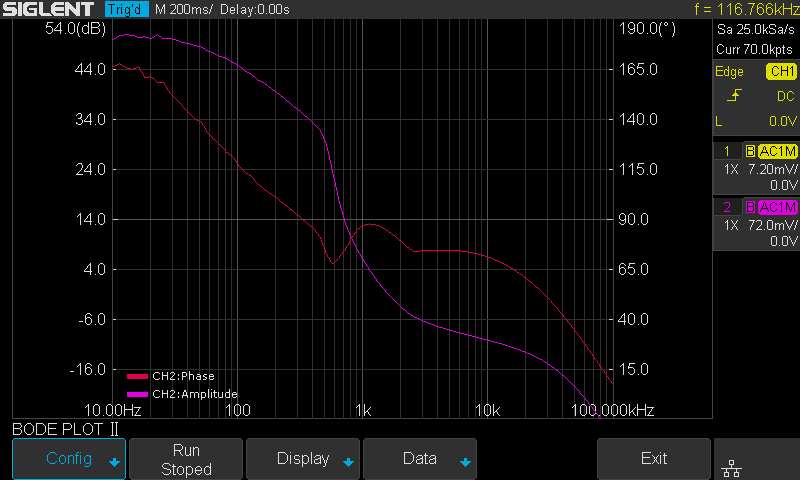 Figure 14: Increased stimulus signal amplitude and distortion
Figure 14: Increased stimulus signal amplitude and distortion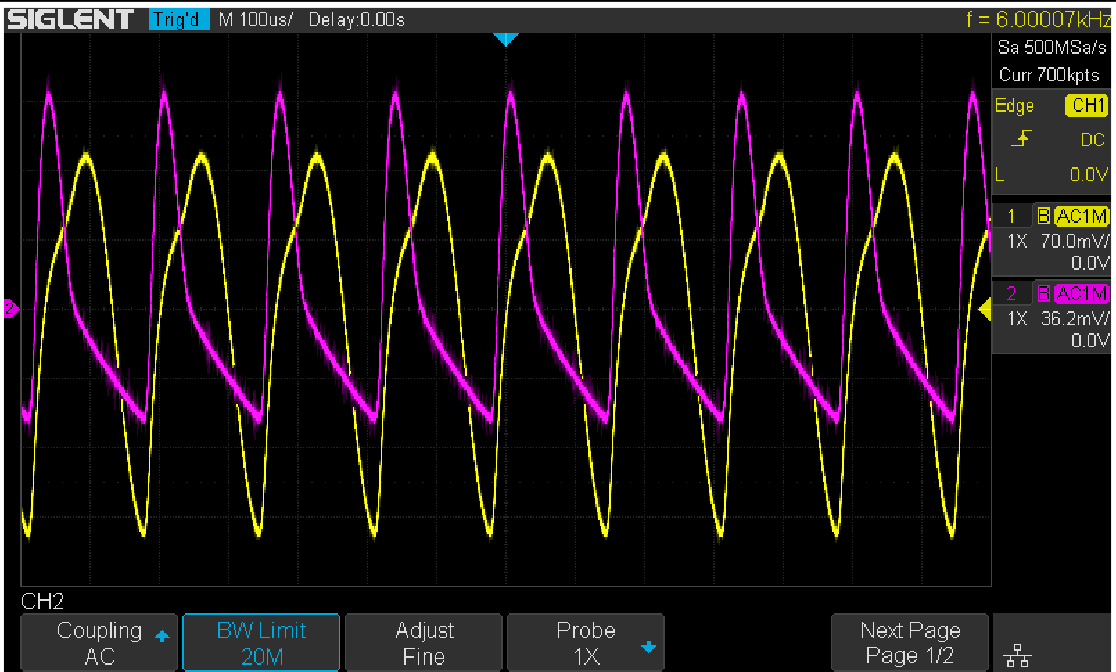 Figure 15: Distortion in the time domain
Figure 15: Distortion in the time domainOne possible solution to the problem is Vari-level (other manufactures may call it “Shaped Level” or “Level Profile”). The Vari-level concept is simple: The stimulus signal amplitude is variable over the frequency. If we use a large signal at low frequencies and decrease the amplitude to a fairly small level near the crossover region so that it causes little distortion to the loop, in theory, we can get an ideal result.
Under the Configure menu, set Sweep Type from Simple to Vari-level, and push Set Vari-level to enter the Vari-level profile editor.
 Figure 16: Set Sweep Type to Vari-level
Figure 16: Set Sweep Type to Vari-levelFigure 17 shows the Vari-level profile editor. The Profile option allows the user to select and save up to 4 profiles. The Nodes sets the number of nodes in the profile trace, the minimum allowed number of nodes is 2 because at least 2 points can determine a line, and always the first and the last node set the start and stop of the trace. Press Edit Table will enter the profile editor mode. The parameter under editing is highlighted by cursors, and next push Edit Table again to cycle the cursors between “Freq”, “Ampl” and the entire row, which allows the user to navigate through the entire table. Users can use the Adjust knob to set the highlighted parameter, and pushing the knob will call out a visual keypad that allows direct input to the parameter. The Set Sweep and Set Stimulus option is somewhat similar to that in the Simple type of sweep, but they are not correlated. This time we set the sweep Mode to Decade and a 40-point-per-decade is sufficient. The profile shown in Figure 17 is used in this measurement. It is not the optimum profile for this circuit but should be a good place to start.
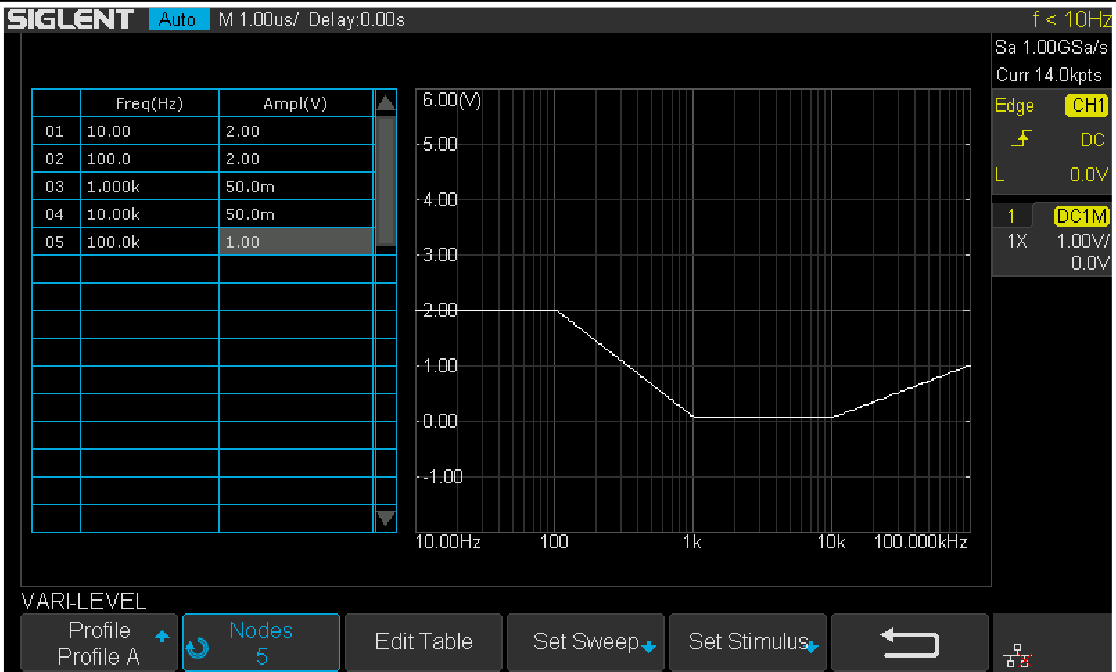 Figure 17: Vari-level profile editor
Figure 17: Vari-level profile editorIn practice, one should always experiment with those parameters to find an optimum solution for a particular circuit.
One practical way to do this is to monitor the signal in the time domain, decrease the amplitude of the stimulus signal until no visible distortion can be observed, then decrease the amplitude by another 6 dB. Next, record the amplitude and frequency, jump to another frequency and repeat the process.
There is a better way to find the optimum profile if you already have a known good profile. Reduce the signal amplitude by 6 dB and run a sweep to see if the plot changes. If it does change, reduce the amplitude by another 6 dB and sweep again. Until the result doesn’t change, then you can increase the amplitude by 6 dB and that’s an optimum profile. This is time-consuming but necessary to get a meaningful result.
Once profile editing is completed, return to the main menu and push Run to start the sweep. Figure 18 shows the final result of the measurement with Vari-level. Changing the capacitor selection switch S1 on the VRTS v1.51 demo board will alter the loop response due to the impact of different capacitors.
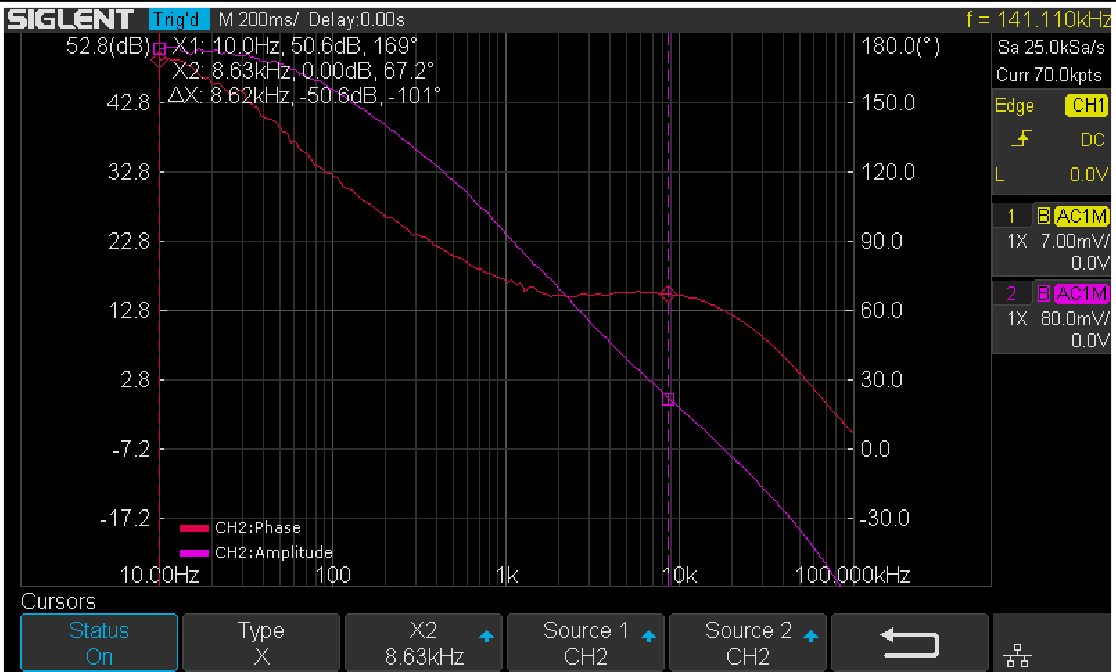 Figure 18: Results with Vari-level
Figure 18: Results with Vari-level3. Summary
The Siglent oscilloscope with newly released Bode Plot Ⅱ together with a Siglent signal generator and a Picotest injection transformer offer a very flexible and easy-to-use power supply control loop measurement system.
Products Mentioned In This Article:
Measuring the Modulation Index of an AM Signal using an FFT
Introduction
In AM schemes, the modulation index refers to the amplitude ratio of the modulating signal to the carrier signal. With the help of Fast-Fourier-Transforms (FFT), the modulation index can be obtained by measuring the sideband amplitude and the carrier amplitude. In this application note, we are going to show a convenient method of using the new Peaks/Markers function (Available on the 4 channel SIGLENT X-E scopes with firmware revisions > 6.1.31).1. Basic Principle
Amplitude modulation uses a signal (typically a sine wave in the audio frequency range from 10 Hz to 20 kHz) to control the amplitude of a higher frequency signal called the carrier.
A carrier with amplitude modulation can be represented as
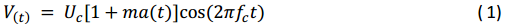
Where:
V(t) The Amplitude Modulated Signal
Uc Amplitude of the Carrier Signal
m Modulation Index
a(t) Normalized Modulation Signal
fc Carrier Frequency
Sinusoidal (commonly referred to as a “sine” wave) modulation is the most commonly used modulation waveform type. If we are using a sine wave, the modulating signal can be expressed as

According to the formulas (1) and (2), we can get
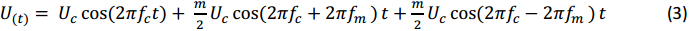
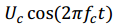 Mathematically represents the carrier waveform.
Mathematically represents the carrier waveform.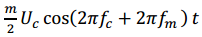 and
and 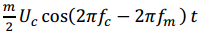
represent the positive, or upper, and negative, or lower, sidebands of the modulated signal.
The amplitude of both sidebands are
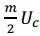
If we set the amplitude of sideband is Us,

In logarithmic case, if the difference between the sideband amplitude and the carrier amplitude is X,

Then the amplitude modulation index can be represented as

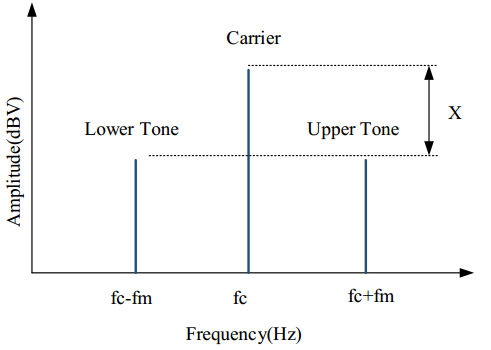
Figure 1
Here, we can see that it is easy to measure the difference between the sideband amplitude and the carrier amplitude, or X. We can then calculate the modulation index very easily.
2. Measurement Setup and Result
2.1 Equipment
Oscilloscope: Siglent SDS1204X-E with firmware version higher than 6.1.31.
Signal Source: Siglent SDG2122X
Cable: 50 ohm BNC
2.2 Instrument Configuration
In this section, we will show how to configure the instruments in order to make the measurement. For complete instructions on the FFT mode, please refer to the oscilloscope user manual and the quick start guide.
The oscilloscope is connected to the output of the signal source as shown in Figure 2.

Figure 2 Set Up for the Measurement
The signal source settings are as follows:
- Mod On
- Mod Type: AM modulation
- Carrier frequency: 1 MHz
- Carrier amplitude: 500 mVpp
- Modulation frequency: 10 kHz, and the modulation index is 80%.
According to the output of the signal source, set the center frequency of the FFT plot to 1 MHz and set the horizontal scale to 5 kHz to provide a clear view of the output.
To reduce random errors, the FFT is set to average mode and the average number of times is 100. On the choice of window function, we choose flat-roofed window to obtain the optimized amplitude accuracy.
Starting with firmware revision 6.1.31, the FFT function of Siglent X-E oscilloscopes include a Peaks/Markers function and users can set the number of FFT points separately. The more points the FFT has, the better the frequency resolution of the plot will have. Note that increasing the number of points will increase the time of computation of the FFT, which will reduce the refresh speed accordingly. FFTs up to 1 Mpts at most are available on the X-E series, so we can set the storage depth to 1.4 Mpts. In this application, there is no need for a high sampling rate, since that will lead to a large delta frequency. Set the timebase to 2ms.
According to the input signal, we can deduce that a frame waveform has 28 k-cycles and we will use the first 20 k-cycles to do the FFT operations. For decent resolution, there should be at least five sample points in a cycle, so the minimum number of FFT points should be at least 100 kpts. 128 kpts is suitable, since under the premise of satisfying the measurement conditions, we can get the results faster.
The new version also supports Peaks/Marker, it can quickly identify and label peaks. We choose Peaks to make the measurement.
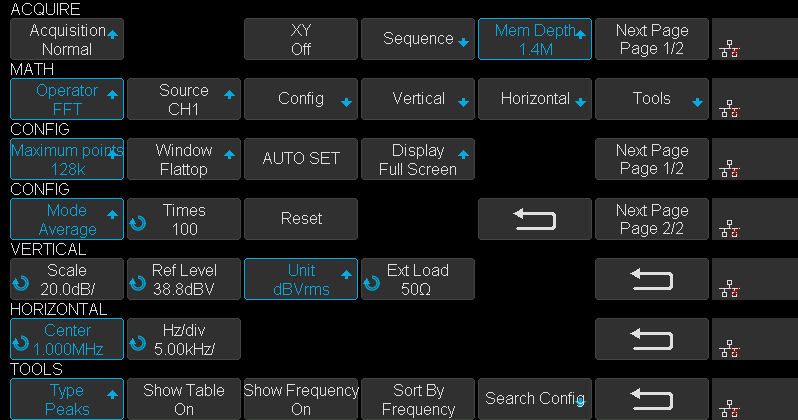
Figure 3 Configuration Screens
The configuration process is as follows:
First, set timebase to 2ms and enter the ACQUIRE menu, set Mem Depth to 1.4M. Second enter the MATH menu, set Operator to FFT, enter the CONFIG menu, set Maximum points to 128k, set Window to Flattop, set Display to Exclusive then go to the next page, set Mode to Average, set Times to 100. Third enter the VERTICAL menu, set Unit to dBVrms, then enter HORIZONTAL menu, set Center to 1MHz, set Hz/div to 5 kHz. Last, enter the FFT TOOLS menu and set Type to Peaks, turn on the Show Table switch to show the peaks list and turn on the Show Frequency switch to show the frequency of peaks, set Sort By to Frequency.
2.3 Result
After configuration is done, enter SEARCH menu, adjust Threshold to show several peaks for easy reading from the table then press Reset. After the average number increasing to 100, the FFT result as shown in Figure 4.
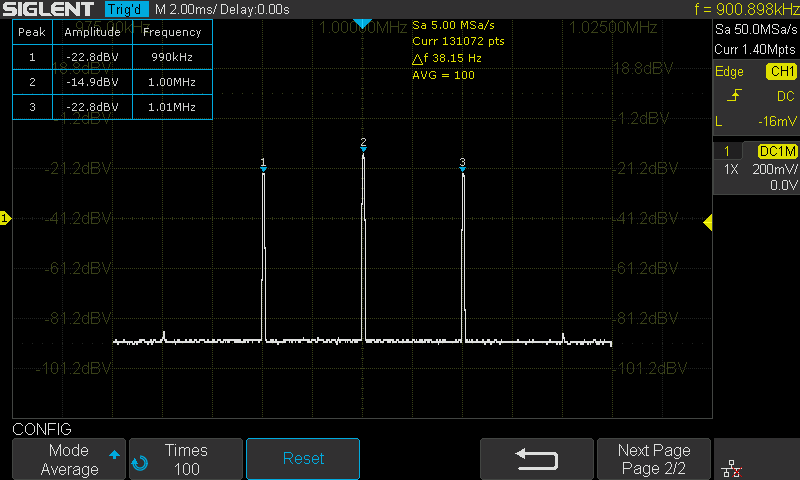
Figure 4 FFT Peaks Result
The carrier amplitude is -14.9dBV, the sideband amplitude is -22.8dBV. So the difference between the sideband amplitude and the carrier amplitude is -7.9dB.
According to the previous introduction, the results of the modulation index are shown in the table 1

3. Summary
The Siglent oscilloscope with newly released Peaks/Markers software, supports peak and harmonic searching which provides a convenient method of spectrum analysis.
Products Mentioned In This Article:
SDS1000X-E Series please see HERE
SDG2000X Series please see HERE
Programming Example: SDS Oscilloscope save a copy of a screen image via Python/PyVISA
Here is a brief code example written in Python 3.4 that uses PyVISA to pull a display image (screenshot) from a SIGLENT SDS oscilloscope via USB and save it to a drive on the controlling computer.
NOTE: This program saves the picture/display image file to the E: drive, which may or may not exist on the specific computer being used to run the application.
Download Python 3.4, connect a SIGLENT SDS Oscilloscope using a USB cable, get the scope USB VISA address, and run the attached .PY program to save an image of the oscilloscope display. The type of file saved is determined by the instruments setting when the program is run.
Tested with:
Python 3.4SDS1102CML+

Products Mentioned In This Article:
Siglent Oscilloscopes please see HERE
Power Supply Design: Load Step Response with a SIGLENT DC Electronic Load
Building a power supply that can handle various loads without oscillating can be a challenge. Computational models and computer simulations can help get your design headed in the right direction, but physical testing is essential to proving the performance of your design.
One method of quickly determining stability is to use a load step response.
In this test, a DC electronic load is used to provide a current load that steps from a low current draw to a higher value in a short period of time. By directly measuring the voltage and current output of the supply with the stepped load, we can visually observe the recovery of the power supply feedback loop and make changes to the design to optimize the response.
For this note, we are going to perform identical tests on two supplies and compare the output voltage and current waveforms: One has been tuned so that the output quickly recovers with minimal overshoot and ringing. The other supply is not tuned and subsequently oscillates. We will also discuss some measurement techniques to help get the right data as quickly as possible.
The Equipment:
A DC Electronic Load: The SIGLENT SDL1020X-E is a 200 W load with dynamic testing capabilities to perform the load step. It also features remote sense capabilities to compensate for the voltage drop across the load leads. High currents can provide a substantial voltage drop across the leads and will add unwanted error.
An oscilloscope: The SIGLENT SDS2354X Plus scope has a large display, easy-to-use interface, and features that make capturing these waveforms very easy.
A power supply: The SIGLENT SPD1168X single output supply delivers power to our power supply board
A current probe: The SIGLENT CP4070 features a 150 kHz bandwidth that will minimise most switching noise from the measurement
Power supplies to test: The Analogue Devices LTM4646 series of uModule Regulators. This module features two 10A DC-DC converters. One has been “detuned” to show some common problems associated with power supply design. The other supply has been left in it’s tuned state as a comparison to the detuned supply.The Setup:
- Connect the SPD bench power supply to the power supply to test and configure the output values to match your supply needs. Here, we set the SPD for 12 V @ 3 A.

- Connect the SDL electronic DC load to the output of the power supply to test. Configure the load for Constant Current (CC), set the voltage and current ranges to the lowest ranges that still accommodate the requirements of the test, set the current load to a value near the maximum for your design. You may also wish to wire up and enable the SDL remote sense which enables remote voltage measurement to minimize the voltage drop caused by the high current flow through the electronic load leads. Here, we set the current to 5 A.

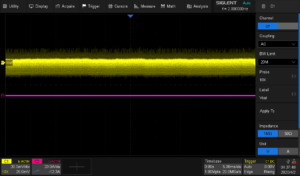
- Connect a passive probe to the oscilloscope CH1. This probe should be connected to the power supply feedback loop to monitor the voltage as the supply adjusts to the load.
- On the oscilloscope, configure CH1 for AC coupling to provide the most resolution to view the feedback voltage which can have high DC offsets. Enabling the Bandwidth Limit (BW limit) can also decrease noise. Here, the SDS2X Plus also has on-screen labels for traces, which can be a convenient way of keeping information organized. Here, I labeled CH1 Vout.
- Connect the current probe to the oscilloscope CH2.
- On the oscilloscope, set the trigger for Rising Edge, CH2 and AUTO. This will allow you to adjust the current probe zero position without dealing with the trigger setting.
- Configure CH2 as a current probe (Units = A), set the Probe attenuation to the proper value (50 mV/A in this case). DC coupling here because we want to see the total signal amplitude. I also applied a label to the output current (Iout).
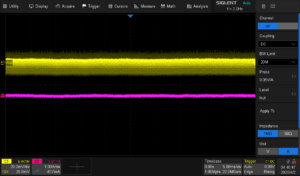
- Zero the current probe. The CPs have a knob that you can use to move the DC offset. Set the scope to a low current range and adjust the probe to get 0 A on the display.

- Clip the current probe around the positive current lead going from the power supply under test to the DC load. Make sure to have the clamp connected such that positive current flow (into the load) produces a positive signal on the scope.
Now, everything is connected and ready to test:

DC Load Verification
Now, you can power on the SPD power supply and SDL load.Make sure that the scope is set to AUTO trigger for now. You can also add an RMS measurement on CH2 so that you can verify the current draw matches the setting on the DC Load.
Here, we have a setting of 5 A on the DC load.. and we show 5 A RMS on the scope:
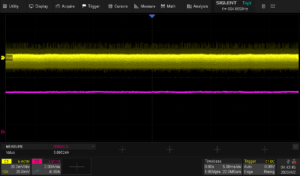
Things are looking good. The current output matches our load setting.
DC Load Step Response
Now, set the DC load to Dynamic Current mode by pressing Utility > CC.. and configure the appropriate ranges, low and high current values and duration, and slew rate for your application.
Here are the settings used for this test:

This will continuously cycle from 1 A for 5 ms to 5 A for 5 ms with 500 mA/us slew rate.
Now, switch the scope trigger mode to Normal and adjust the vertical, horizontal scales and positions.. as well as the trigger level to get a stable trigger and a few periods of transition on the display:
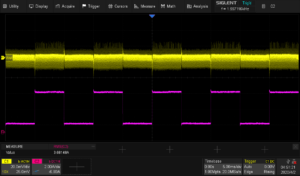
Verify that the supply high and low current values match the setpoints. For this example, we have 1 A for 5 ms and 5 A for 5 ms.. which is what we observe.
Observe and Optimise
Now, let’s compare a tuned setup to one that is not tuned for our load as well as some techniques to gather more information about the response.
First, you likely see quite a bit of noise on your signal. The majority of this is due to switching noise in the supply being tested. Here is a zoomed image of the feedback voltage where you can see the switching noise quite clearly.
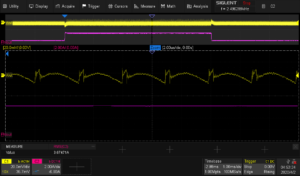
Enabling waveform averaging can help:
Now, we see the output voltage from CH1 (yellow), output current from CH2 (pink/purple), and the average voltage math function (orange):
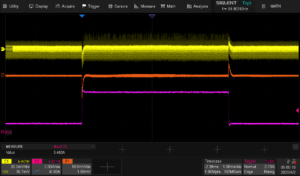
This is the tuned setup.
Now, let’s look at a detuned supply:
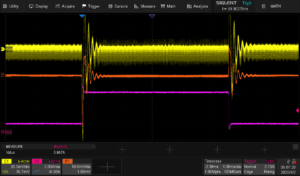
The scaling on these two images is exactly the same. You can see a large amount of ringing associated with the detuned supply. This design is very close to becoming an oscillator with this load. If our step duration was any shorter, the supply voltage wouldn’t be settled and our output would be very poorly regulated.
Here are some closer images of the rising and falling edges on shorter time scales:
Tuned, Rising:
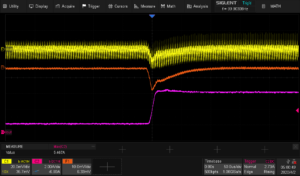
Tuned, Falling:
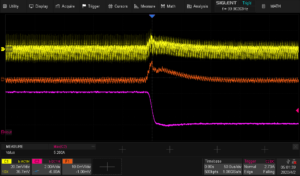
Detuned, Rising:
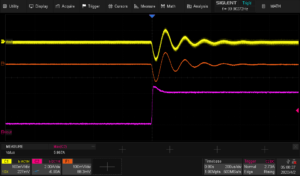
Detuned, Falling:
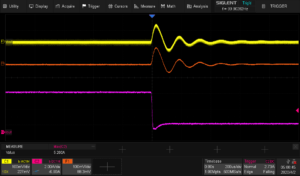
Conclusions
A DC load step test can quickly show you the performance and stability of a power supply design. Using a few common pieces of test gear, you can ensure that your design is ready to undertake the most challenging application requirements.