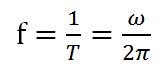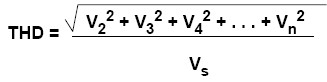Your cart is currently empty!
Tag: Siglent Function Generators
Programming Example: Create a stair-step waveform using Python and PyVISA using LAN (SDG1000X, SDG2000X, SDG6000X)
The SIGLENT SDG series of arbitrary waveform generators can use waveforms created programmatically.
The waveform data can be sent as individual samples formatted as binary little-endian, 2s complement values.
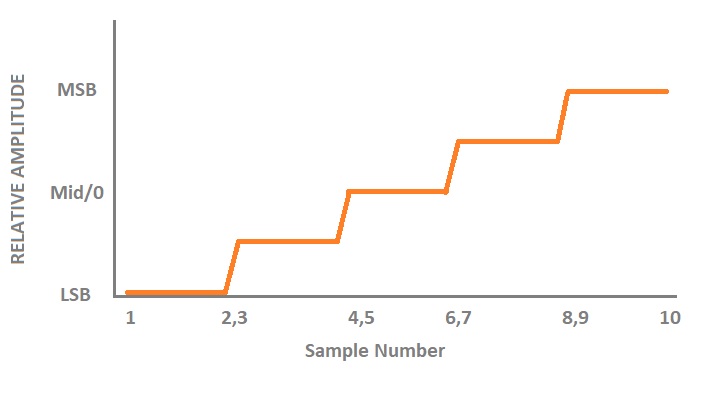
In this programming example, we create a 10 point arbitrary waveform that starts at the least-significant bit and steps up to the most-significant bit to help with understanding the required sample format as well as provide a base for your own waveform creation.
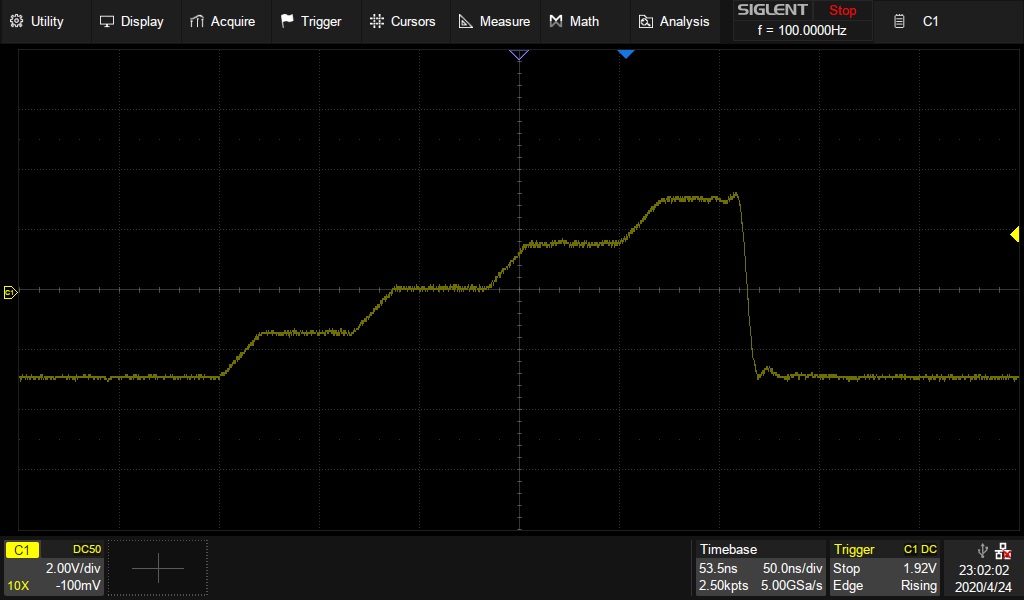
Here is a picture of the desired waveform:
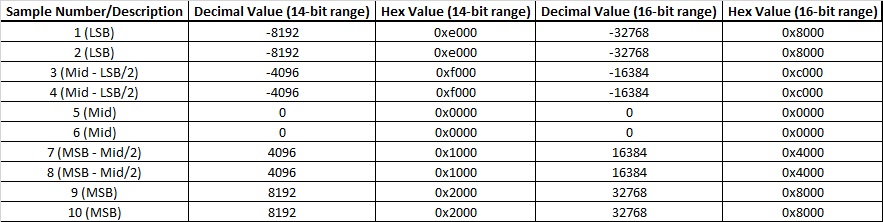
 The SDG waveform data requires each sample to first be formatted as binary, little-endian, 2’s complement. For easier human viewing, the example enters the data in hex format and then “unhexes” the data before it is added to the command string which is then sent to the instrument.
The SDG waveform data requires each sample to first be formatted as binary, little-endian, 2’s complement. For easier human viewing, the example enters the data in hex format and then “unhexes” the data before it is added to the command string which is then sent to the instrument.Here is a table showing the value of each sample and the value in hex for 14-bit (SDG1000X series) and 16-bit (SDG2000X/SDG6000X) instruments:
Here is an oscilloscope capture of a single burst of this waveform:
Products Mentioned In This Article:
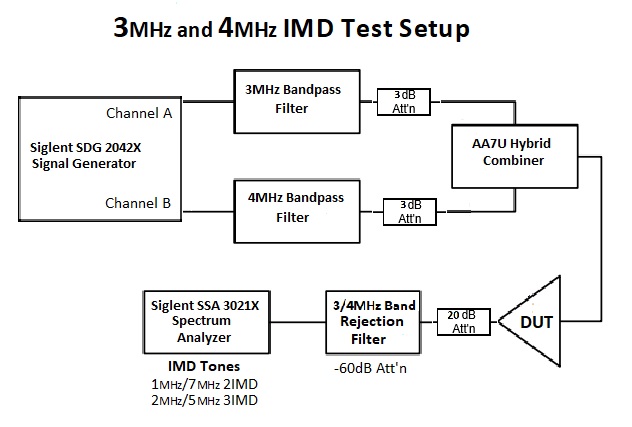
Inter Modulation Distortion (IMD) testing
Two SIGLENT SDG owners and Amateur Radio operators and frequent experimenters, Steve Ratzlaff AA7U and Everett Sharp N4CY, got together and built a very thorough test procedure for testing Intermodulation Distortion (IMD) on a Loop Amplifier using a SIGLENT SDG2042X generator and SSA3021X spectrum analyser.
IMD is an important test for verification of audio amplifiers and radio receivers as high IMD can cause audible distortion that can decrease the quality of the transmission.
In this experiment, AA7U and N4CY use a SIGLENT SDG2042X generator to deliver the IMD tones and a SIGLENT SSA3X spectrum analyser to measure the result.
They also build some filtering to help decrease the harmonic content of the generator and build a coupler with better performance than commercially available products.
***

Siglent SDG2042X (AWG) Dual Channel Arbitrary Waveform Generator set up for use in IMD Test Set
- Turn on the AWG (arbitrary waveform generator) — wait for it to initialise.
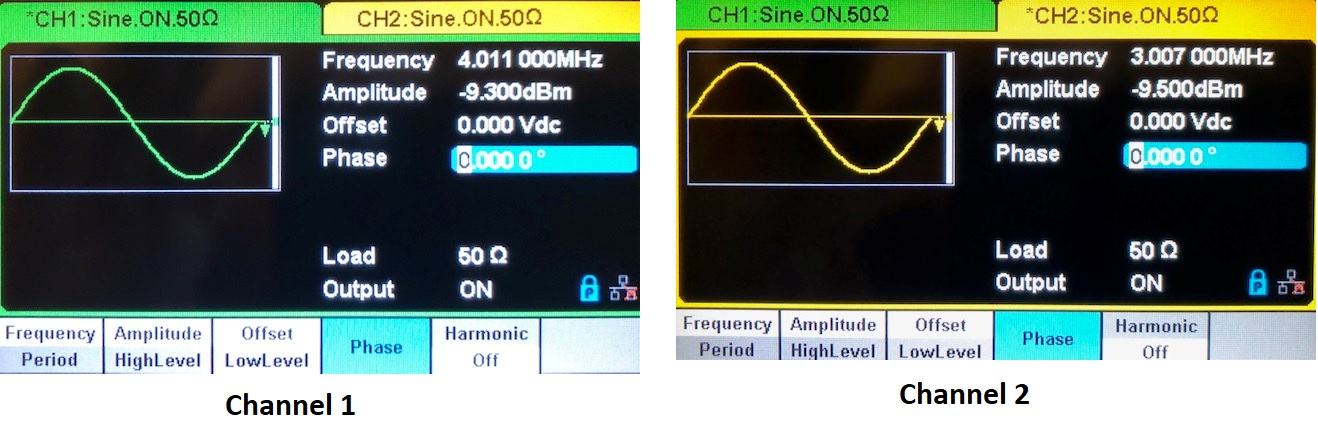
- Frequency is highlighted, with 1 kHz the default. Enter “3”, then touch “MHz” at the bottom left. (By touching the screen where it says Frequency, you can enter the frequency on the keypad “3” then at the bottom of the screen touch “MHz” and that will set the frequency).
- You will need to be set to 3 MHz (3.007 MHz) on Channel 1 and set 4 MHz (4.011 MHz) on channel 2 (Note: The reason for using the odd frequencies is the Siglent SSA3021X (SA.. or Spectrum Analyzer) has a sub-harmonic spur at 5 MHz)
- Load–HI Z is the default. Select “50 Ω” at the bottom, by touching the screen.
- Amplitude–2.00 Vpp is the default when in 50 ohms load. Enter “0”, then touch “dBm” on the bottom (fifth one over from the left–Vpp; mVpp; Vrms; mVrms; dBm). Make sure to set dBm.
- Output–OFF is the default. Touch it and it turns ON and the Ch1 indicator turns on with the button also, by its BNC connector.
- Repeat the above for Ch 2 as described above.
- Adjust Amplitude settings for each channel, which are going through the Band Pass Filter (BPF), 3 dB attenuator, combiner and DUT under test for a 0 dBm on the SA, with the SA internal Attenuator set at -20 dB.
(Note: As an example, this will be around (~ -10dBm). Make sure that the 3 MHz BPF is connected to the 3.004 MHz Channel and the 4 MHz BPF is connected to the 4.011 MHz Channel.
IMD Test Setup–Spectrum Analyzer setup for Siglent SSA 3021X
There are two parts to the setup–the first part sets the levels at the DUT output to 0 dBm; the second part measures the IMD.
Part 1
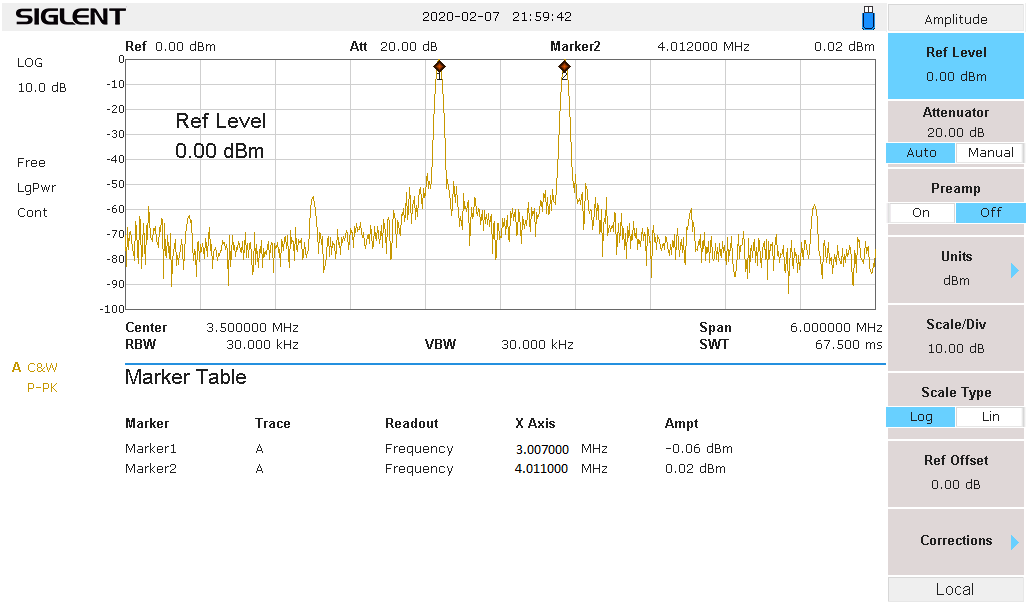
(Calibration) Push “Preset”, Top Right, to set up for initial setup.
Set Center Freq 3.5 MHz, Span 6 MHz, Amplitude Ref Level +10 dBm
- Connect the DUT (Power On) output to SA input. Tune to one, either the 3 MHz, or 4 MHz test tones on the AWG. Adjust the generator (AWG) for 0 dBm on the SA, within 0.1 dB. Tune to the other test tone, adjust the generator for 0 dBm.
SA: Recheck each tone again to make sure nothing has changed. This concludes the initial setup.
Part 2
- Disconnect the DUT output from SA and connect it to the Reject Filter input (Which has the 20 dB built-in Attenuator). Connect the Reject Filter output to SA RF input.
2. Now look at the 4 IMD frequencies.
-
- Span set to 1 kHz
- Amplitude turn Preamp Off; set Ref Level to -60 dBm, Set Attenuation to Manual and set Attenuation to 0.00 dB.
- Push the Trace button and look for and select “Avg Times 100”, which is located on the right bottom side of the screen.
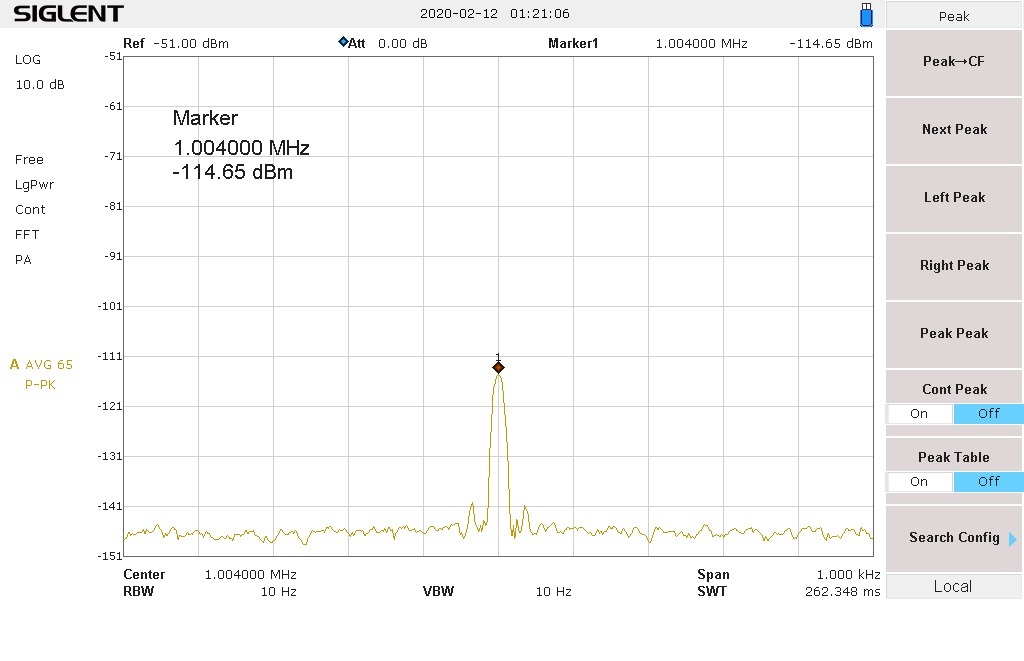
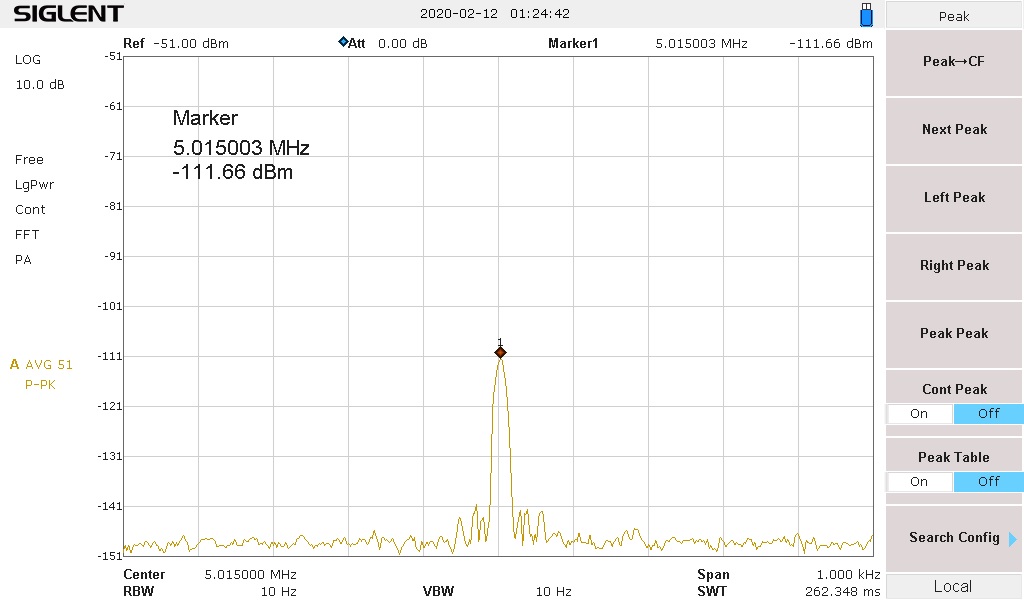
The 4 frequencies you will be looking at are: Center Freq 1 MHz (1.004 MHz), 7 MHz (7.018 MHz), 2 MHz (2.003 MHz) and 5 MHz (5.015 MHz),
- You should now be seeing the 2IMD product in the center of the display 1 MHz (1.004 MHz). Push the Peak button or push Marker button and use the main tuning knob to tune to the peak of the signal. It will probably vary up and down, but wait for 100 averages and decide what the middle value is and write that down.
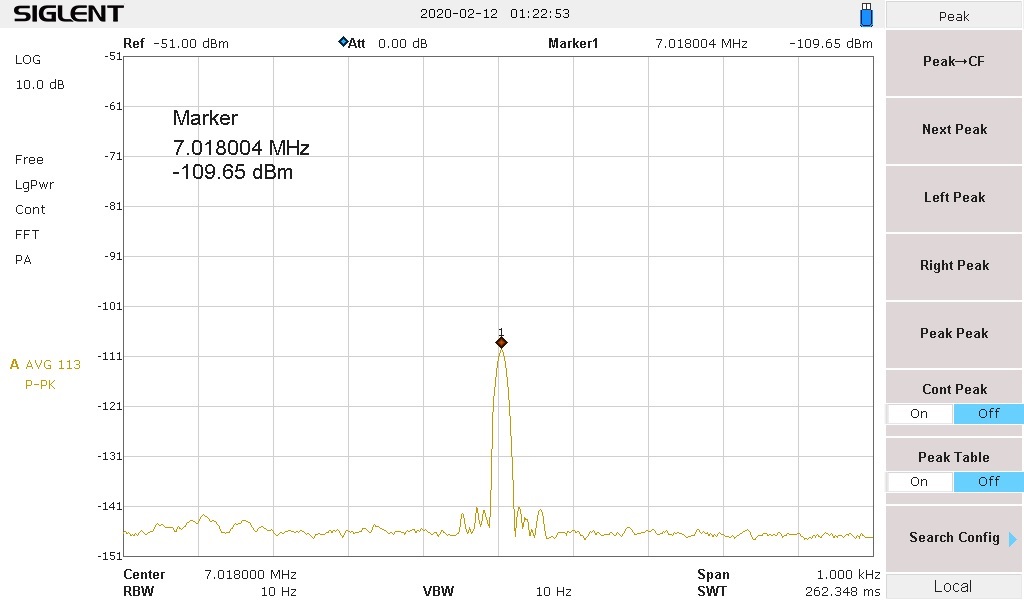
- Tune to the 7 MHz (7.018 MHz) 2IMD product and note its level–write that down.
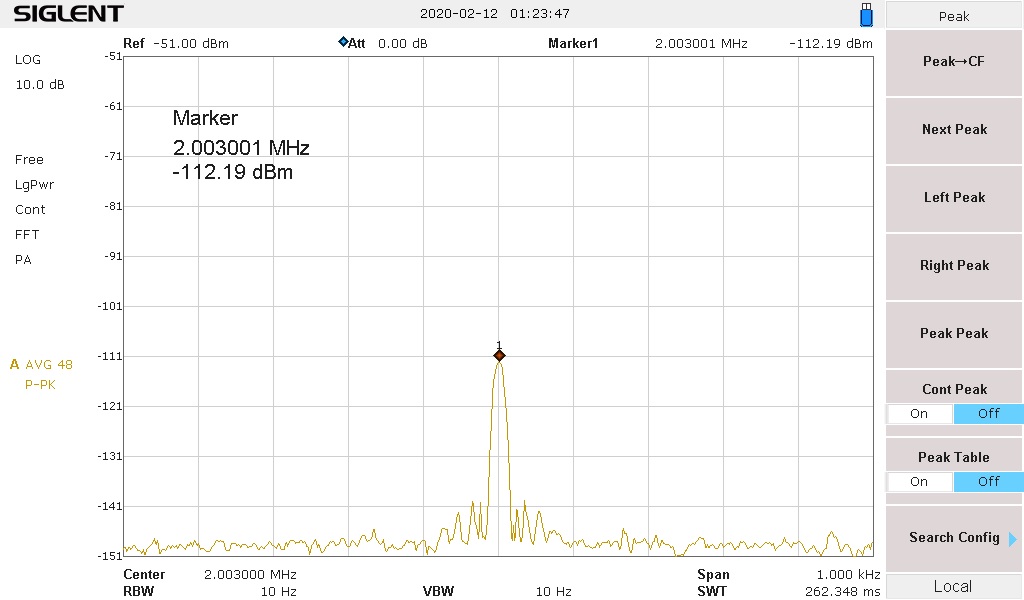
- Tune to 2 MHz (2.003 MHz) 3IMD product, this will normally be much weaker, where the SA’s preamp may be needed to see it. Write down that level.
- Tune to 5 MHz (5.015 MHz), write down that level. You now have measured the four IMD levels.
Use the formula for determining OIP2. (2IMD level – Reject Filter loss at that frequency 1 and 7 MHz) = OIP2.
Determine the OIP2 for both 2IMD frequencies. They are usually different–use the worst case, or specify both Output Intercepts.
Use the formula for OIP3. (3IMD level – Reject Filter loss at that frequency 2 MHz and 5 MHz) /2 = OIP3. Determine OIP3 for both 3IMD frequencies. Usually, they are about the same.
Examples
My reject filter has a -21.6 dB loss at 1 MHz; -20.39 dB loss at 7 MHz for the 2IMD frequencies. There is a -20.65 dB loss at 2 MHz and -22.62 dB loss at 5 MHz for the 3IMD frequencies.
The examples used in the below calculations were taken from the above IMD sweeps.
1 MHz (-109.65 dBm) – (-21.6 dB loss) = (109.65 – 21.6 = 88.5) = +88.05 dB OIP2.
7 MHz (-111.66 dBm) – (-20.39 dB loss) = (111.66 – 20.39 = 91.27) = +91.29 dB OIP2.
Normally you take the worst case and state that, which would be +88.05 dB
2 MHz (~-112.9 dBm) – (-20.65dB loss) = (112.9 – 20.65) = 92.25/2 = +46.13 dB OIP3.
5 MHz (~-111.66 dBm) – (-22.62 dB loss) = (111.66 – 22.62) = 89.04/2 = +44.52 dB OIP3.
Normally these should be very close, otherwise take the worst case, which would be +44.62 +dB
and state that.System IMD Intercept Test with Band Pass Filters, Combiner and 3 MHz and 4 MHZ Band Rejection Filter connected to the SA
They are all at the noise floor, which is very good. It took adding Band Pass Filters in place of Low Pass Filters to achieve the results Below.
1 MHz (1.004 MHz) -151.26 dBm
7 MHz (7.018 MHz -152.45 dBm
2 MHz (2.003 MHz) -153.51 dBm
5 MHz (5.015 MHz) -152.26 dBm
These are the simple formulas for second and third order IMD, you can take any two frequencies and work out the IMD products
Second order: F1 + F2; F2 – F1
Third Order: 2F1 + F2; 2F1 – F2; 2F2 + F1; 2F2 – F1
3 MHz and 4 MHz tones: 3 + 4 = 7 MHz ; 4 – 3 = 1 MHz; 6 + 4 = 10 MHz; 6 – 4 = 2 MHz; 8 + 3 = 11 MHz; 8 – 3 = 5 MHz
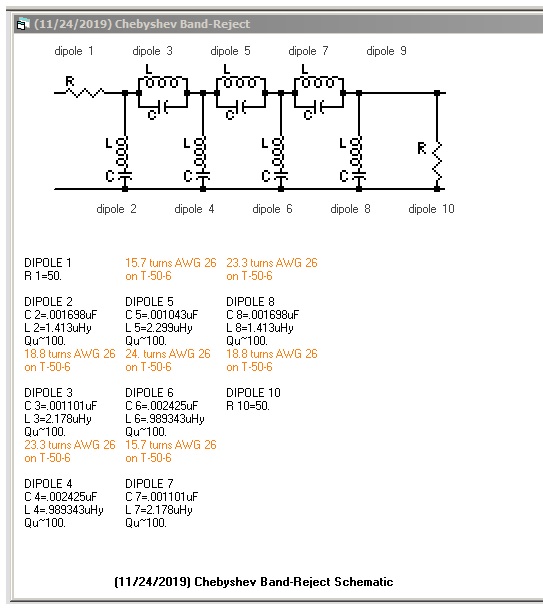
Building the Bandstop Rejection Filters
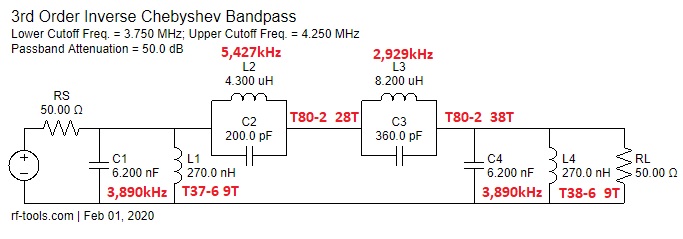
The easiest way to build and tune this filter is to test each Dipole (Tuned Circuit) by its self. It should be 3,250 kHz. Below is a sweep from my VNA, as this is what I used to check and tune each Dipole. I was able to tune the parallel circuits by having one side soldered to its pad and then connect the other end after tuning. You can also use the SIGLENT SSA3000X, SSA3000X Plus, or SVA to tune the filter.. as shown in this note on Filter Testing Using a SIGLENT Spectrum Analyser
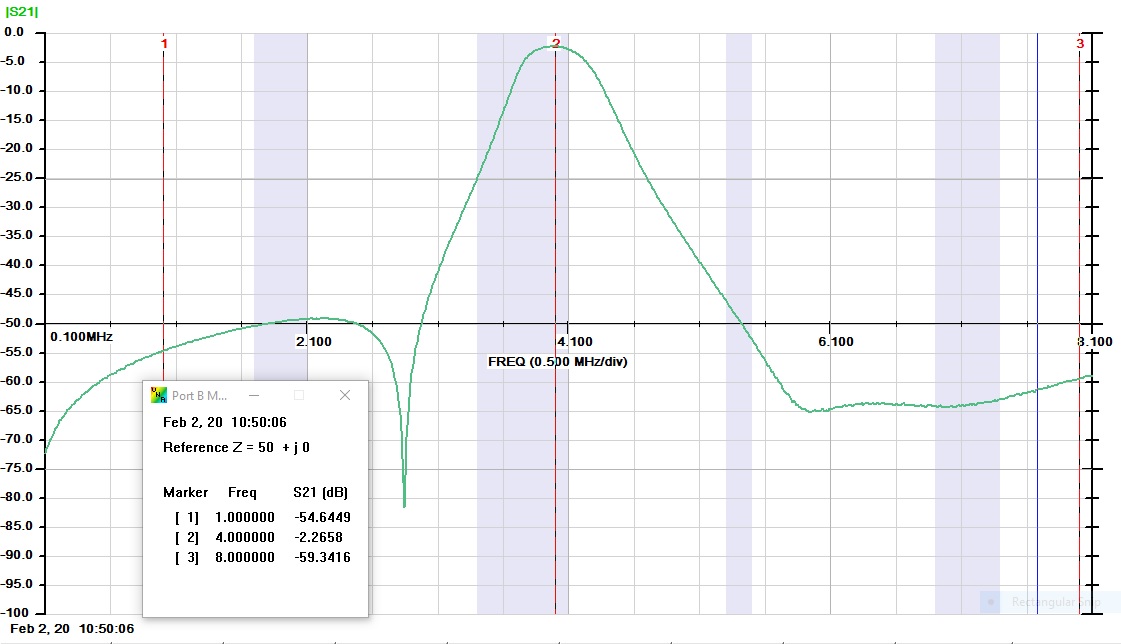
Below is a sweep of the final Band Rejection filter that is being used for IMD testing. There is around 58 dB rejection for 3 and 4 MHZ
Below is the finished 3/4 MHz Bandstop Filter and Sweep
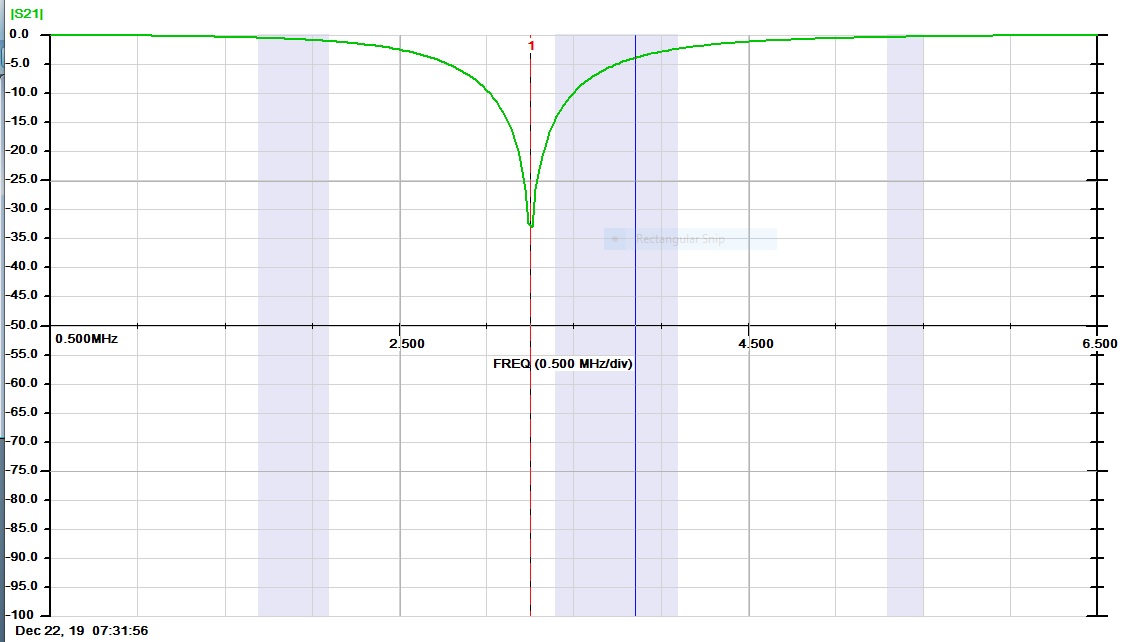
Below is a sweep of the final Band Rejection filter that is being used for IMD testing. There is around 58 dB rejection for 3 and 4 MHZ

A 20 dB pi pad can be done with 62 ohms shunts and a 270 ohm in parallel with 3300 ohms for the series resistor. (249.6 shown on the diagram. The theoretical value is 248 ohms.)
Both the 3 MHz and 4 MHz Bandpass filters are easy to build if you will tune each pole and install it as you go. I have marked the frequencies in Red for each pole. Also, I have indicated which Micrometal Toroids that were used with the turns required for each pole. You may have to make some adjustments to each of the poles, as there are variations from lot to lot with the toroid core. I also found it helpful to use an LCR meter to make adjustments in the turns count to get the desired inductance. I used an Array Solutions VNA2180 to tune each pole and evaluate the final filter. A SIGLENT SVA1000X VNA can also be used.
4 MHz BPF
3 MHz BPF

AA7U Hybrid Combiner
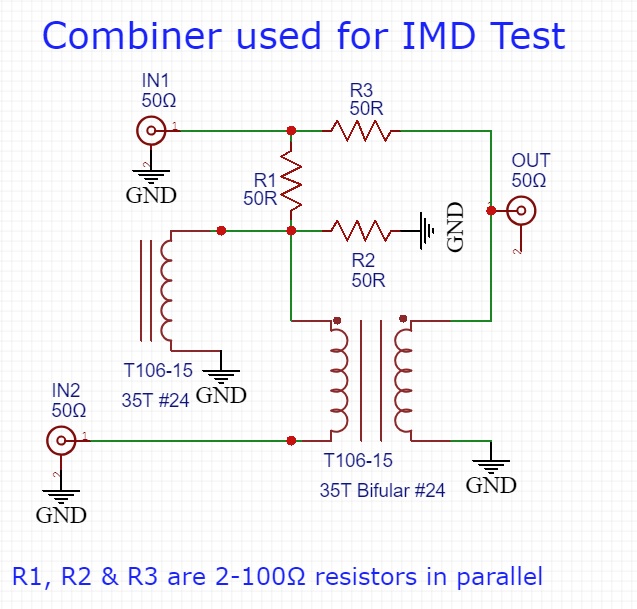
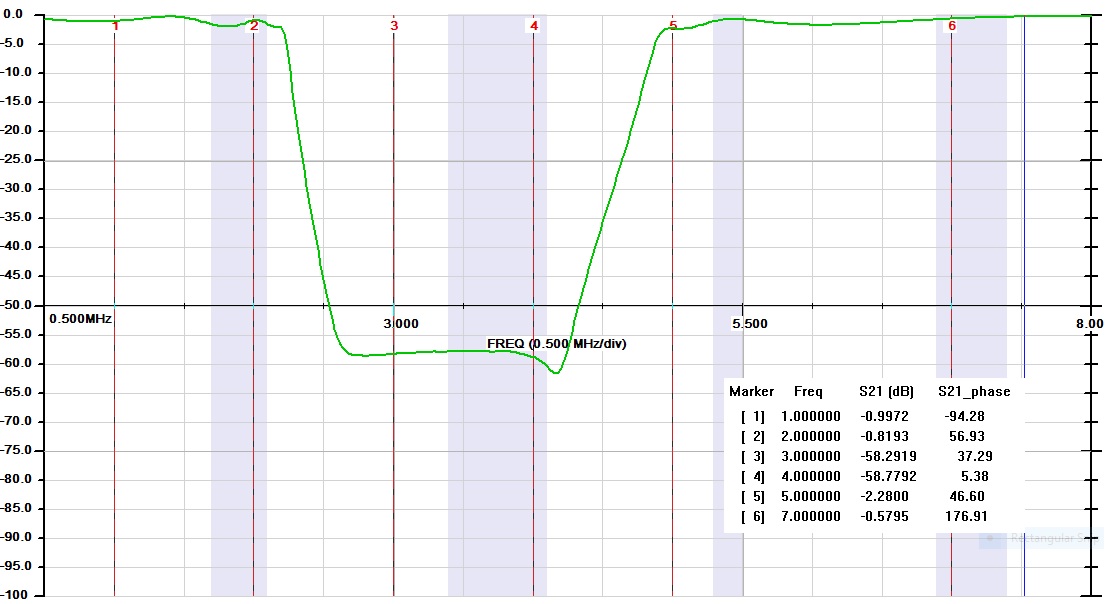
The loss through the filter is 6.13 dB/5.95 dB and the isolation between the two input ports is 74.58 dB at 3 MHz and 73.97 dB at 4 MHz (Measured with a 50Ω Termination at the output port.) After completing and testing the filter I filled it up with hot melt glue.

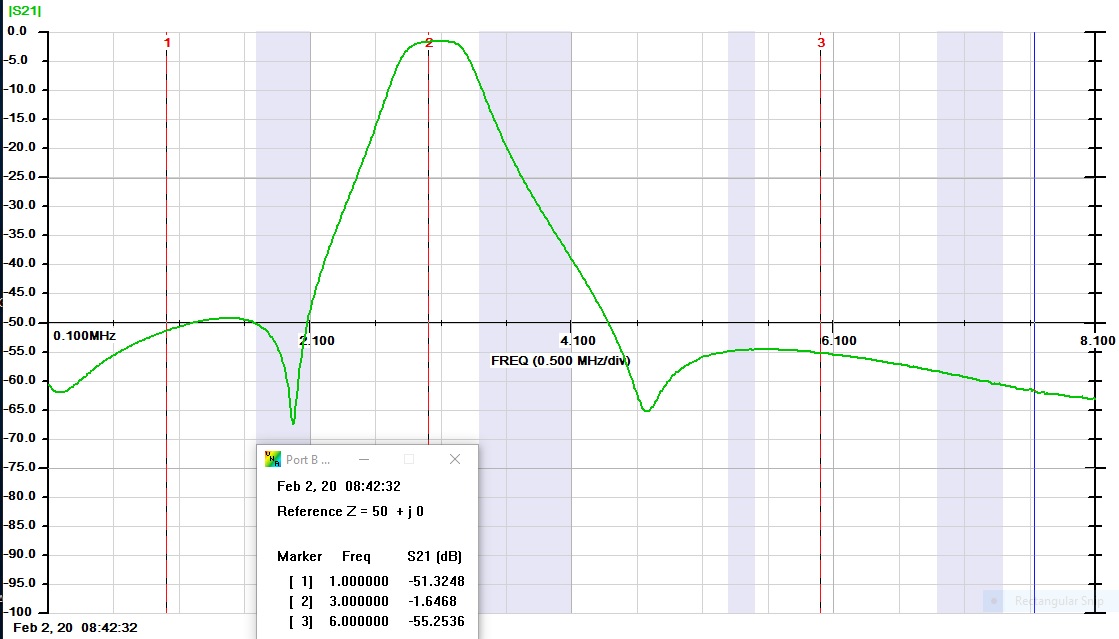
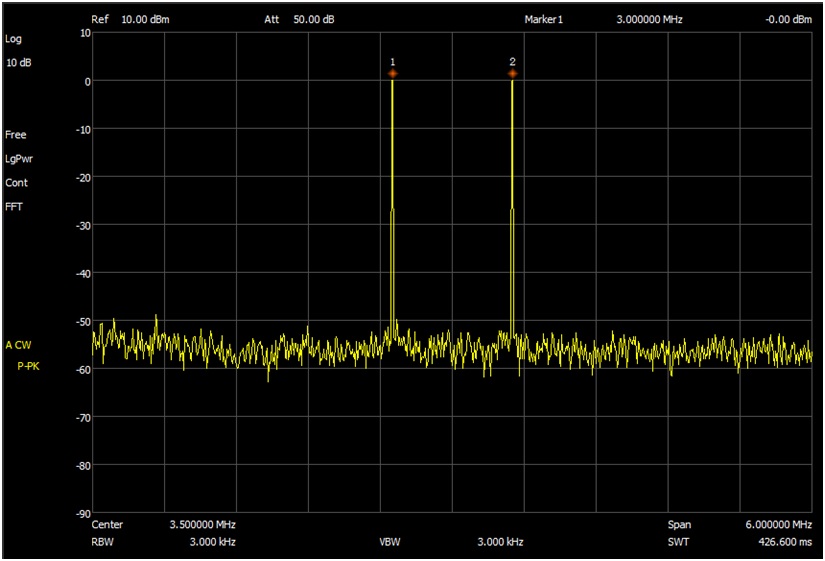
Below is a sweep of the Hybrid Combiner between the two input ports and it was terminated with 50Ω at the output port.
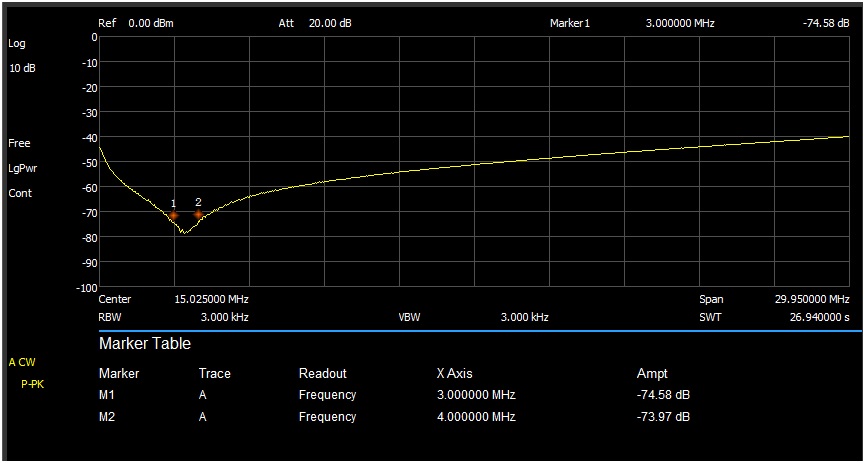
This is a sweep showing the two test tones 3 MHz and 4 MHz using the Hybrid Combiner. Notice how sharp they are.
How to take screenshots of the Siglent SA
Insert the thumb drive into the front USB port of Siglent.
You should see a blue USB icon in the upper right-hand corner of the screen.Hit the File button
You should see a file directory similar to what you would see on a PC.Under the Folder column, you should see two directories:
Local: free 80.74 MB (your size may be different)
+U-disk0: 748.00 KB/975.88 ME (your size may be different)On the right-hand side soft keys, the “Save Type” should be PNG.
Hit the button and select JPG (or whatever file type you want – CSV, LIM, JPG, BMP, etc.)Rotate your frequency tune knob and select your +U-disk0 directory
You should see the files currently on your thumb driveHit the Enter button
Hit the Operate button
Hit the Marker button
You should now be back at your main display screenSetup a screen that you want to save
Hit the Save button
A pop-up window will show you a default file name of Name: JPG1 and an Input type: abc
I like to use a numeric file name, so I hit the +/- button
Now I backspace out the default “JPG1” file name
I enter the numeric name that I want to use. Example: 111
I find it quicker to use quick numeric file names and rename the file once the thumb drive is attached to my PCHit the Enter button
You may or may not see a brief text message on the screen about the screen being saved to your thumb drive.To confirm that the file was saved to your thumb drive, Hit the File button
Use the Frequency control knob and select your thumb drive directory
In the directory listing for the thumb drive, you should see your recently saved screen snapshotFor some reason, the screen sometimes saves to the internal Siglent memory. When this happens, I go through the steps again about setting up a save to the thumb drive. I suspect that my steps are a little flakey in this area.
Once the Flash drive is set up you can save the screenshots by pressing the Save button, which will number the shot and then press the Enter button.
Products Mentioned In This Article:
- SDG2000X Series please see HERE
- SSA3000X Series please see HERE
- SSA3000X Plus Series please see HERE
- SVA1000X Series please see HERE
Multi Channel function generator synchronisation
1. Introduction
Multi-channel function generators are useful in many situations. For example, in Radar testing the generator needs to output several phase coherent signals and for the phase to be independently adjustable for each signal. In 3-phase power line harmonic distortion testing, a 4 channel generator is required to simulate the multiple voltages and currents.
1.1 Problem
A standalone multi-channel generator can be very expensive.
1.2 Solution
Siglent provides the Multi-Device Synchronisation function in the SDG1000X, SDG2000X, and SDG6000X generators. This allows synchronization among several units in order to output signals with adjustable steady phase relationships. Thus saving on cost.
2. Setup of Synchronisation
2.1 Wiring
Multi-Device Synchronisation will require the use of the Aux In/Out and 10 MHz In/Out rear-panel interfaces to implement the synchronisation. First, all the generators’ Aux In/Out BNC connectors need to be connected together. Next, connect the Master unit’s 10 MHz Out to the Slave unit’s 10 MHz In. Please note that the SDG6000X family has separate 10 MHz In/Out outputs, so more than two units can be synchronized. The wiring interconnection concept is shown in Figure 1.
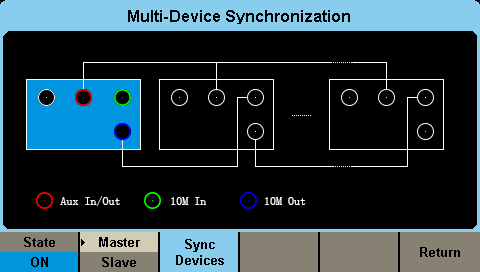
Figure 1. Wiring concept
However, the SDG2000X and SDG1000X series’ 10 MHz In/Out ports share one connector. Therefore, only two units can be synchronized together or they must be the last Slave unit in a multiple units connection.
In this note, the SDG2000X and SDG6000X series models are used as our example. The SDG6000X will be the Master device.
1) First connect two units’ Aux In/Out with BNC cable. See in Figure 2.

Figure 2. Connect SDG2000X and SDG6000X Aux In/Out
2) Next connect the SDG6000X 10 MHz Out port with the SDG2000X 10 MHz In/Out port, as shown in Figure 3.

Figure 3. Connect Master 10 MHz Out to Slave 10 MHz In
2.2 Parameter settings
Set the waveform parameters, such as Frequency and Amplitude, on 4 all channels. More information on this step can found in the User Manual.
Press Utility, go to Page 2/3, choose Phase Mode, and then set both units as Phase Locked.
In this example we are setting all 4 channels as a 1 kHz, 4 Vpp square wave. CH3, CH4 signals viewed on the SDS5000X oscilloscope are output by the Slave generator, note that the phase is drifting. Open the Display/ Persist function to track it on the scope, as shown in Figure 4.
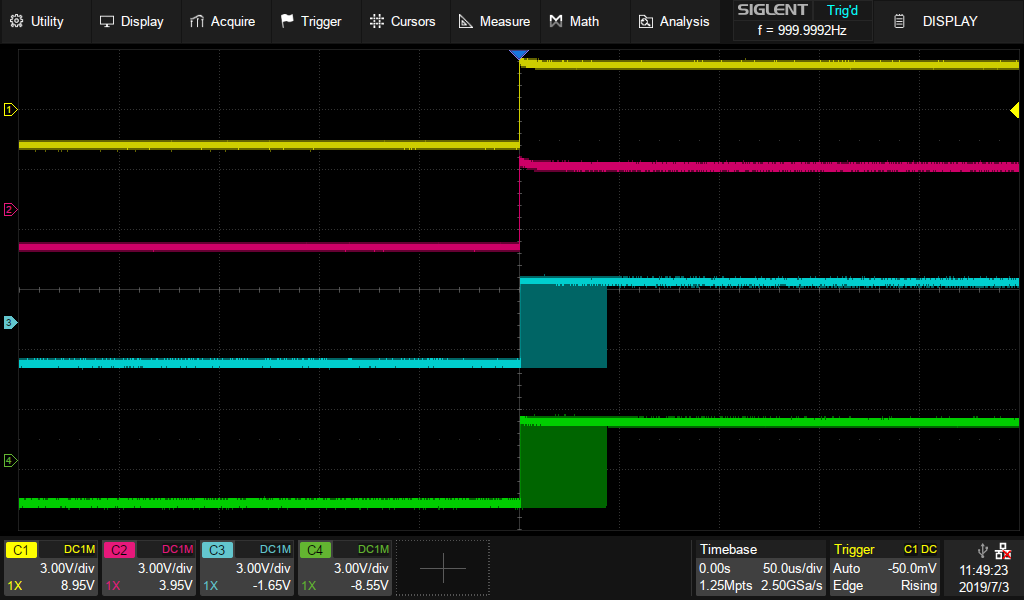
Figure 4. Four signals phase drift without synchronisation
2.2.1 Set Master Device
1) Press Utility button, go to Page 3/3, then press the soft key under screen to select Multi-Device Sync. The menu will enter the Multi-Device Synchronization screen, shown in Figure 5.
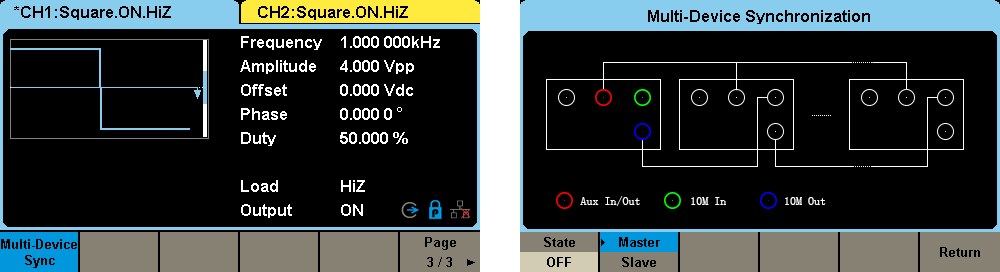
Figure 5. Multi-Device Synchronisation Screen
2) Press the soft key under the screen to turn on/off this function and select it as either the Master or Slave. The Multi-Devices Synchronisation menu will appear when turned on. When ”Master” appears shaded in light gray this means the device is designated as the Master device, as shown in Figure 6. When this device is set to be the master, its clock source is automatically set to internal and the 10 MHz output is enabled.
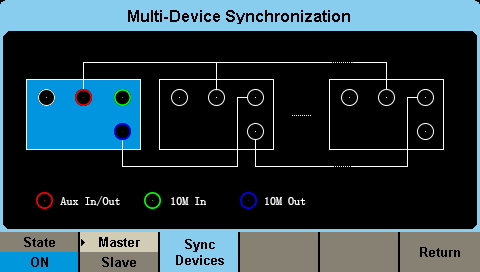
Figure 6. Turn on synchronisation function
2.2.2 Set Slave Device
1) Enter into the Multi-Device Synchronisation menu. Select it as Slave, Slave will be shaded in blue, as in Figure 7. As the device is set to a slave device its clock source is automatically set to external.
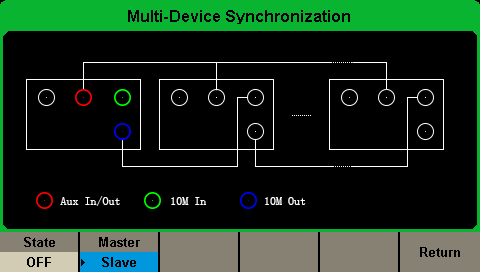
Figure 7. Select the unit as Slave device
2) Turn on the State. Then the Slave Device Delay window will occur. Press to enter delay value, as shown in Figure 8.
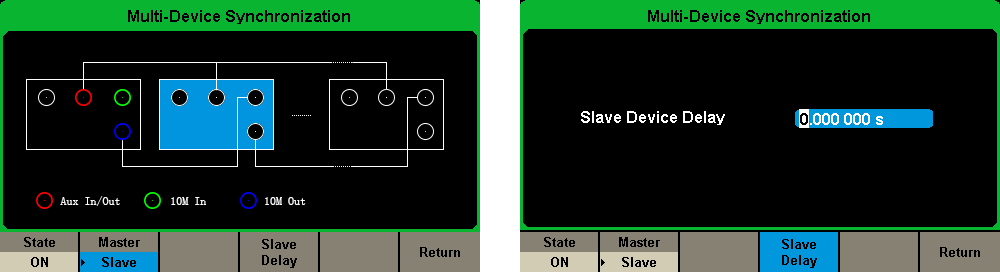
Figure 8. Set the Slave Delay
2.2.3 Synchronise the Devices
Press the soft key ”Syncs Devices” in the Multi-Device Synchronisation interface of the Master device, as shown in Figure 1, to begin synchronisation between the master and slave devices. Anytime a setting is changed; for example, the Slave Device Delay, ”Sync Devices” must be pressed to activate the new settings.
3. Measure on an Oscilloscope
3.1 Slave Device Delay measurement
1) Turn on Synchronisation on both units, measure the Skew between CH1 and CH3. As in Figure 9.
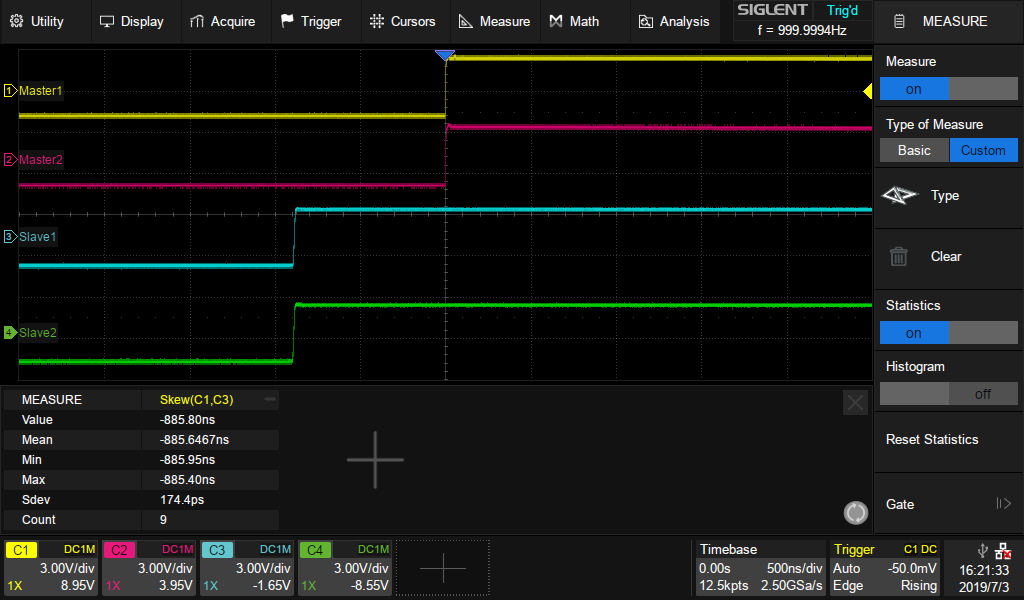
Figure 9. Measure the Skew between Master and Slave Devices
2) Enter the absolute Mean value of Skew into Slave Device Delay. This will eliminate the delay between traces that we observed with our oscilloscope. See Figure 10.
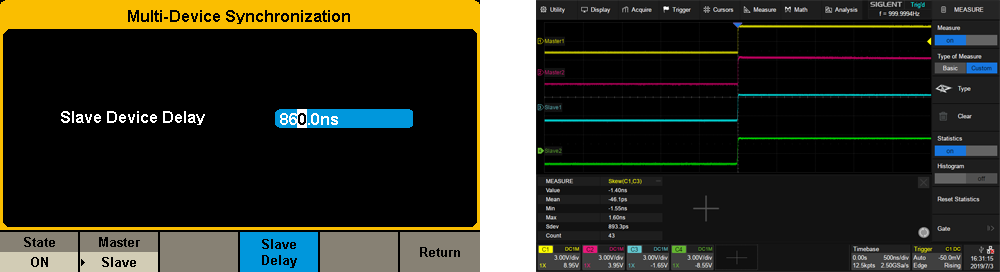
Figure 10. Eliminate the Slave Delay
3.2 Adjust phase relationship
Set CH1 Phase as 0 degree, CH2, CH3, CH4 Phase as 180, 270, 360 degrees, respectively. The result is shown in Figure 11.
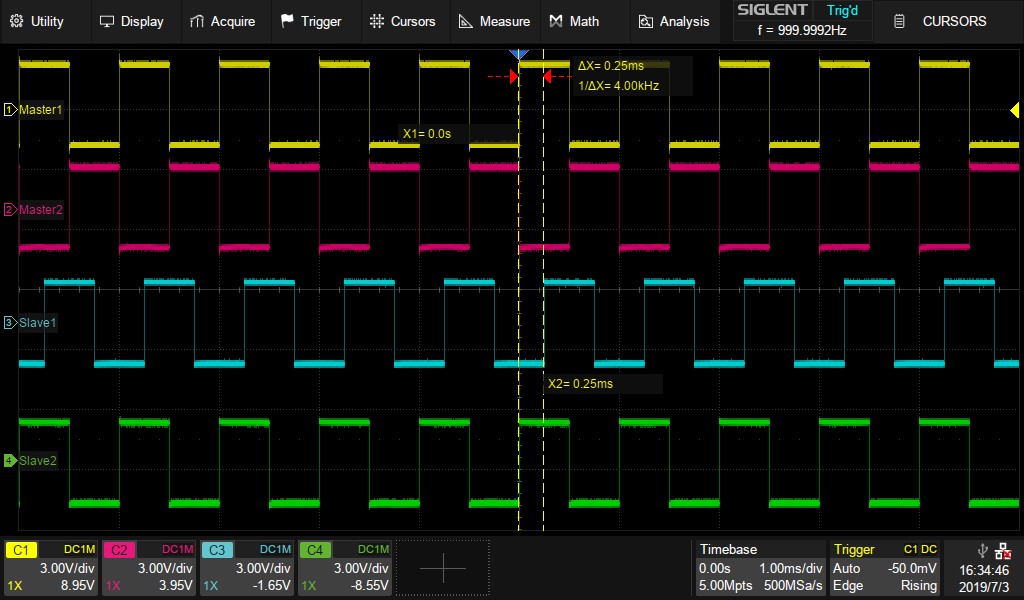
Figure 11. Adjust phase relationship
Products Mentioned In This Article:
Secure products without K-lock slots
Many products have Kensington, or K-lock slots to help provide a location to secure a cable lock or other device to help prevent theft.
Some products do not have locations for cable lock connections.
In this case, we recommend using a special glue or physical attachment system to secure the cable to the case of the instrument.
Here is an example:
https://www.kensington.com/p/products/security/lock-anchor-points-accessories/security-slot-adapter-kit-for-ultrabook/
AWG Basics
Many electronic designs feature the ability to monitor or measure input signals and then perform another task or function based on that input signal. A simple example could be a circuit that looks for an input voltage to exceed a specific amount and triggers another action after it occurs. In such cases, having the ability to configure and deliver a known or simulated signal can be a critical addition to testing the performance of the design. Unlike acquisition instruments that measure a signal, an input signal can be created using a signal source. This can be as simple as a DC power supply or as complex as a digital communication signal delivered by an RF Vector Source. One of the most flexible and useful signal sources available today is the Arbitrary Waveform Generator (AWG).
In this series of notes, we are going to introduce some of the features that make AWGs so useful and explain in a bit more detail just how they work.
What types of signal sources are on the market today?
Let’s start with the basics. Most sources can be divided into two broad application categories: Digital and Analogue.
Signal sources specially created for digital applications are often called logic sources. Logic sources can be roughly divided into two categories: Pulse and pattern generators. A pulse generator can output square waves and pulse streams. The output frequency of the pulse generator is generally very high and it is often used to test digital devices. A pattern generator, also known as a logic source or data generator is a bit unique. This kind of instrument generally has 8 or 16 output channels, but higher channel counts are available. Each output can generate various types of synchronous digital pulse streams, generally from a low to a high voltage value, 0-5 V for example. Pattern generators are often used as excitation signals for computer buses, digital telecommunications units, and other serial communications links.
Analog generators typically have one or two outputs and feature a wider array of possible output levels, wave shapes, and frequencies than digital sources. More specialised forms of analogue generators also exist for high frequency applications. We aren’t going in to further detail about them here, but some common types include RF signal generators, microwave signal generators, and baseband signal generators.
In this article, we will concentrate on the most general purpose signal source, the arbitrary waveform generator. In simple terms, an arbitrary waveform generator is a device that creates an output signal based on a digital waveform file, created from a series of discrete output sample points, and “plays” the file contents at the source output of the generator. Using this sampling principle, waveforms of almost any type can be created, including basic waveform functions like square, sine, and ramping output shapes.
Arbitrary waveform generators can also have more advanced functions like output triggering and system clock signals for synchronizing external instruments. One such generator is the SIGLENT SDG2000X series function / arbitrary waveform generator shown in Figure 1 below.
Figure 1: SIGLENT SDG2000X function / arbitrary waveform generator
What is the waveform generator used for?
As mentioned previously, most arbitrary waveform generators include basic function types like sine, square, and triangle waves. In addition, waveform generators can also generate analogue and digital modulation signals, supporting the output of linear / logarithmic sweep signals and pulse trains. Many of SIGLENTs SDG series of generators support AM, FM, PM, FSK, ASK, DSB-AM and other analogue and digital modulation functions and include a large standard library of included arbitrary waveform functions.
There are hundreds of applications for waveform generators, but in the field of electronic test and measurement, the application range can be basically divided into three types: inspection, verification, and limit / margin test. During the commissioning phase of a design, the engineer needs to test the parameters of the product to verify whether the product meets the relevant design specifications. In this process, the waveform generator can be used to source the signal specified in the design specification. Here, the Engineer can observe the response of the design, compare the results with the specifications, and perform any adjustments that may be necessary with the design. In addition, newly developed industrial control modules, data conditioning modules, and others all need to use waveform generators to test their linearity and monotonicity through exhaustive testing. In many occasions, the waveform source needs to add a known, repeatable distortion in quantity and type to the signal it provides. With many generators, you can add noise and programmed distortion to the signal and directly test the ability of the design to handle specific real-world signal issues.
What are the main indicators of the waveform generator? What do these indicators mean?
Oscilloscopes have common banner specifications: Bandwidth, memory depth, and sampling rate. When we select a suitable oscilloscope, these three major indicators are often our first consideration.
Does the waveform generator also have the so-called three major indicators? The answer is yes. In the category of waveform generators, there are also concepts of bandwidth, sampling rate and memory depth.
- Bandwidth
The bandwidth of the waveform generator is often defined as the maximum frequency of a sine wave. Unfortunately, what applies for a sine wave may not apply to other waveform types. For example, the maximum sine wave output frequency of the SIGLENT SDG2122X is 120 MHz, while the square wave has a maximum frequency of 25 MHz. The reason for this difference is that a square waveform transitions very quickly from one voltage value to another. Faster transitions require that the waveform contains many higher-frequency components than the smooth transitioning sine wave. In order to avoid heavy distortion of the rising edge of the square wave output, when the waveform generator outputs a square wave, its bandwidth range must be able to include these higher harmonic components.
- Sampling rate
The sampling rate of the waveform generator is usually expressed in mega-samples (MSa/s) or giga-samples per second (GSa/s). For example, the nominal sampling rate of SDG2000X series function / arbitrary waveform generator is 1.2 GSa / s. This parameter indicates the output rate of each sample of the waveform being sourced. The Nyquist sampling theorem stipulates that the sampling rate or clock rate must be at least twice the highest spectral component of the generated signal, thus, accurate reproduction of the original signal can be guaranteed. But in practical applications, twice is often not enough, depending on the type of signal and the rise time. Higher output sampling rates indicate that a signal source is capable of sourcing samples quickly. Low sample rates can limit a generators ability to accurately source a given waveform type.
Here is a quick example.
If you have a waveform made of 1,000 samples and your generator can source 10 MSa/s, the maximum output frequency of the waveform can be calculated as follows:
Frequency = Sample Rate/Samples = 10 MSa/s / 1000 Samples = 10 kHz.
So, the sample rate and number of samples used to create your waveform determine the output waveform period and can be a quick test to determine if the generator will work for your application.
- Memory depth
Memory depth refers to the number of data points used to record the waveform, which determines the maximum number of samples of the waveform data. The bandwidth of the waveform generator is determined by the sampling rate and memory depth. The SDG2000X series function / arbitrary waveform generator supports “point-by-point output”, which can output 8 pts ~ 8 Mpts at a variable sampling rate of 1 uSa / s ~ 75 MSa / s without losing waveform details. Deeper memory provides higher resolution in the time domain and enables users to create more detailed waveforms.
In addition to the above three indicators, frequency resolution and vertical resolution are also important indicators of waveform generators. Vertical resolution refers to the smallest voltage increment that can be programmed in the waveform generator, and is related to the number of DAC bits used in the hardware circuit. It is generally expressed in units of “bits”, which determines the amplitude accuracy of the output waveform. Frequency resolution, the smallest adjustable frequency resolution, that is, the smallest time increment that can be used when creating a waveform, is related to the highest rate of the clock and the conversion rate of the DAC.
The waveform generator is one of the most widely used basic general-purpose instruments and it is an indispensable tool for simulating signals and testing your design performance. For more information, search out our additional articles to give you more understanding of the principles of the waveform generator.
Products Mentioned In This Article:
SDG2000X Series please see HERE
The basic output waveform and related parameters of the arbitrary waveform generator
Traditional function generators can output standard waveforms such as sine waves, square waves, and triangle waves. However, in actual test scenarios, in order to simulate the complex conditions of the product in actual use, it is often necessary to artificially create some “irregular” waveforms or add some specific distortion to a waveform. Traditional function generators can no longer meet the requirements and an arbitrary waveform generator may be a good option.
Arbitrary waveform generators can easily replace the function generators. They can source sine waves, square waves, and triangle waves like a standard function generator. In addition, they can also output pulse, noise, DC signal types, modulated signals, sweeps and bursts. Many arbitrary waveform generators currently on the market are equipped with arbitrary waveform drawing software. Through this software, theoretically, the arbitrary waveform generator can be remotely controlled to output all the signals required in the test process.
So, what types of waveforms can an arbitrary waveform generator output?
What parameters are available for an arbitrary waveform?
How to measure the quality of the output waveform?
- Sine Wave / Cosine Wave
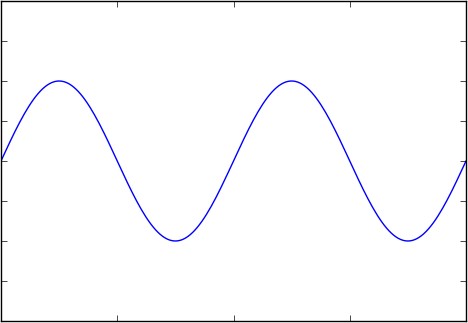
Figure 1 Sine wave / Cosine wave
Sinusoidal (sine) and cosine waves are the two most familiar waveforms in electronics.
Sine/cosine waves are defined as follows.
OR
Where A represents the amplitude of the sine wave,
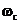 represents the angular frequency, and
represents the angular frequency, and  represents the initial phase, which can be omitted in the general calculation. The sine and the cosine waves are essentially the same, but the initial phase differs by 90 °.
represents the initial phase, which can be omitted in the general calculation. The sine and the cosine waves are essentially the same, but the initial phase differs by 90 °.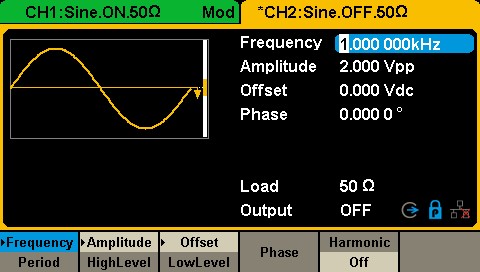
Figure 2 Sine wave setting interface in SDG1000X
These three parameters are as shown in Figure 2. The frequency and period related to the angular frequency can be set in the arbitrary waveform generator, and the conversion relationship between them is:
The frequency of a generator, like the SIGLENT SDG2122X function / arbitrary waveform generator sine wave can be set up to 120 MHz. Usually, the nominal maximum output frequency of the arbitrary waveform generator often refers to the maximum frequency of its sine wave output.
You can also set the amplitude, A. When the output impedance is set to the “high impedance” state, the maximum output amplitude of the SDG2122X can reach 20 Vpp.
The initial phase can be set by clicking the corresponding button in the [Phase] menu. The range of the initial phase can be set between -360 ° and + 360 °.
From the time domain perspective, the parameters and waveforms of the sine and cosine waves are relatively simple. However, all electronic devices have more or less distortion, and arbitrary waveform generators are no exception. Let’s observe sine and cosine waves in the frequency domain.
The Fourier transform corresponding to the time domain function represented by Formula 1 is:
The spectrum diagram represented by Formula 4 is shown in the figure below:

Figure 3: Cosine spectrum/frequency domain
Looking at the cosine spectrogram (showing amplitude vs. frequency) in Figure 3, we can find that the frequency of a sine/cosine wave can be represented by a single line on the spectrum. Signals that occupy only one frequency are called “monotone” because they only have one frequency component.
In engineering, due to the non-ideal characteristics such as the non-linearity of the circuit, the generated sine wave is often not an ideal monotone signal, but may contain other frequencies. Collective “unwanted” frequencies are often lumped together under the term distortion. Some common contributors to distortion are harmonics and spurs.
- Harmonic distortion
The fundamental frequency of a signal is the lowest frequency component of a periodic signal. Harmonics are the frequency components of the signal that are integer multiples of the fundamental. Distortion is the ratio of signal power to maximum harmonic power, usually in dB, as shown in the following figure:
Figure 4: Harmonic distortion
Another index to measure the performance of harmonic distortion is total harmonic distortion (THD), which refers to the ratio of the root mean square of the amplitude of each harmonic (usually taken to the 6th harmonic in engineering) to the signal amplitude, as shown in Formula 5, usually expressed in %. When an SDG2000X outputs 0 dBm, 10 Hz ~ 20 kHz sine wave, the total harmonic distortion is 0.075% at most.
- Non-harmonic spurs
In addition to harmonics, the distortion caused by nonlinearity may also be some other spectral components, such as the intermodulation products of the signal (or its harmonics) and the clock signal. It is necessary to define other index-non-harmonic spurs to measure.
The size of the spur is usually expressed by the spurious-free dynamic range (SFDR) (see Figure 5), which refers to the ratio of the signal power to the maximum spurious power. The unit is usually dB. Please note that the definition of spurs in some places includes harmonic and non-harmonic spurs, but in arbitrary waveform generators, spurs only refer to distortions other than harmonics.
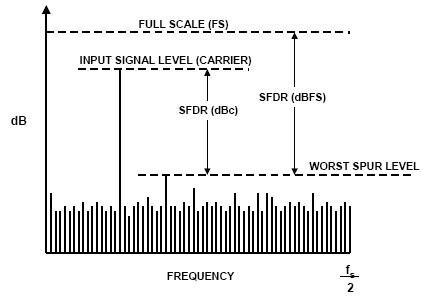
Figure 5: SFDR
Products Mentioned In This Article: